BD=1,2 (единиц), CD=3,6 (единиц)
Объяснение:
По условию точка D отрезка BC находится в 3 раза ближе к точке B, чем к точке С, означает что точка D делит отрезок BC в отношении 1:3. Отсюда отрезок BC делится на 1+3=4 равные части, из них 1 часть соответствует длине отрезка BD, а 3 части длине отрезка CD.
Длина BC = 4,8 и поэтому одной части, то есть длине BD, из 4 равных отрезков соответствует 4,8:4 = 1,2 единиц, а 3 частям, то есть длине CD, 3·1,2 = 3,6 единиц.
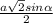
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

BD = 1.2; CD = 3.6;
Объяснение:
Пусть BD = x , тогда CD = 3x и BC = BD + CD = 4x.
По условию ВС = 4,8
Уравнение: 4,8 = 4х
х = 4,8 : 4
х = 1,2 - длина отрезка BD
3х = 3 · 1,2 = 3,6 - длина отрезка CD