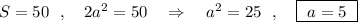Б) Гіпотенуза і катет прямокутного трикутника відносяться, як 5:3. Через вершини трикутника і центр вписаного в нього кола
проведено парастыі прямі до перетину з площиною, що не має з
трикутінком слі:Iьних точок. Довжини відрізків цих прямих від
кінців більшого катета, починаючи від вершини прямого кута, до
пощини дорівнюють 27 і 36 см, а від третьої вершини — 29 см.
Обчислити довжину відрізка від центра вписаного кола до ціа
LIOTHEE
ответ: h=5 см .
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции :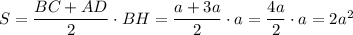
По условию: