Для удобства будем ставить элементы креста по одному. Для начала ставим белый центр наверх и на кубике находим 4 ребра с белым цветом: бело-красное, бело-оранжевое, бело-синее и бело-зеленое. После этого выбираем любое, его мы и будем ставить первым. У нас может возникнуть несколько ситуаций, каждая из которых рассмотрена на картинках ниже.
Если ребро стоит в среднем слое, то просто движениями R или L' ставим их к белому центру.
Но это место может оказаться уже занято другим ребром с белым цветом, поэтому мы должны отвести его в сторону при поворотов U, U' или U2 и поставить нужное нам ребро уже знакомыми поворотами R или L'.
Если же ребро окажется на верхнем или нижнем слое, то движениями F или F' ставим их в средний слой и делаем R или L', как и до этого.
Также ребро может оказаться в нижнем слое и белым цветом смотреть вниз. В таком случае ставим свободное место наверху над ним и поднимаем ребро движением F2.
Таким образом нужно поставить к белому центру все 4 ребра.
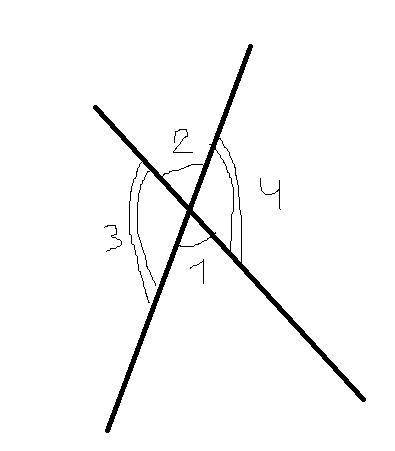
При пересечении двух прямых образуются только углы двух видов: смежные и вертикальные.
Перпендикулярные прямые рассматривать смысла нет: все углы по 90° и условие не выполняется, поэтому есть 2 тупых и 2 острых угла.
У смежных углов сумма равна 180°.
То есть даже на примере:
∠1 смежен с ∠3 и ∠4, то есть ∠1+∠3=180°, ∠1+∠4=180°
Аналогично ∠2 смежен с теми же углами. И ∠1=∠2.
И это явно не могут быть 2 тупых угла, так как они как вертикальные равны между собой, но если ∠3+∠4=140° и ∠3=∠4, то ∠3=∠4=70°, а они тупые, то есть такого быть не может. Поэтому это могут быть только ∠1 и ∠2, которые равны по 70° и являются друг для друга вертикальными.
Что и требовалось доказать.
7.6-2см=4.4 сумма двух боковых
Одна боковая равна =4.4:2=2.2см)
Врлед так