Объяснение:
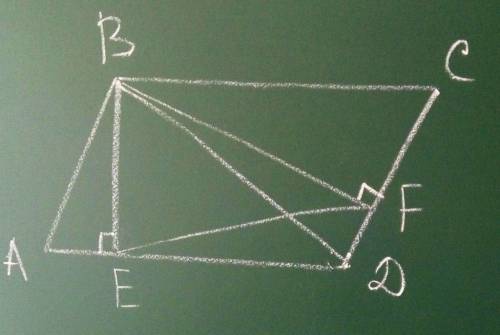
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.
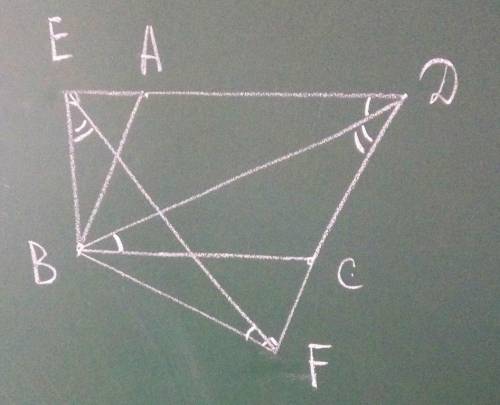
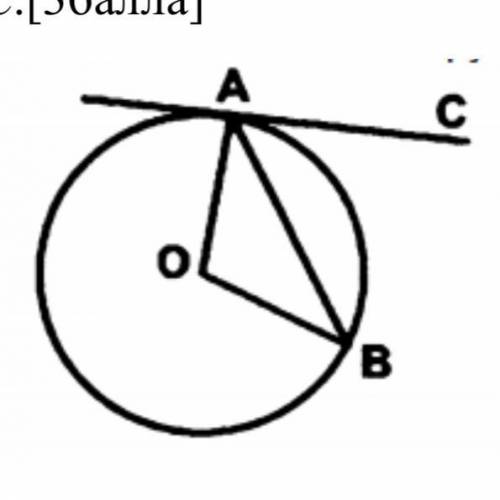
Радиус ОА перпендикуляр к касательной АС,поэтому
<ОАС=90 градусов
Треугольник АОВ равнобедренный,т к
АО=ОВ,как радиусы,значит
<ОАВ=<В=(180-120):2=30 градусов,
как углы при основании равнобедренного треугольника
<ВАС=90-30=60 градусов
Объяснение: