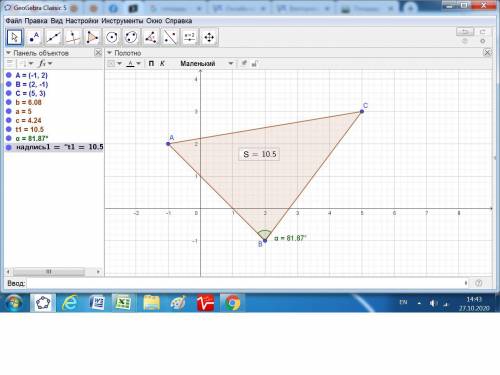
Даны точки А(-1;2), В(2;-1), С(5;3).
Вектор АВ = ((2-(-1)); (-1-2)) = (3; -3), модуль равен √(9+9) = √18 = 3√2.
Вектор АС = ((5-(-1); (3-2)) = (6; 1), модуль равен √(36+1) = √37.
cos a = (3*6 + (-3)*1) / (3√2*√37) = 15/(3√74) ≈ 0,58124.
Угол А = 54,46223°.
Угол В аналогично.
Вектор ВА -3 3 модуль 3√2
Вектор ВС 3 4 модуль 5
cos b = (-3*3 + 3*4) / (3√2*5) = 3/(15√2) ≈ 0,14142.
Угол B = 81,87°.
Площадь треугольника равна половине модуля векторного произведения.
Находим векторное произведение.
i j k| i j
AB 3 -3 0| 3 -3
AC 6 1 0| 6 1 = 0i + 0j + 3 k -0j - 0i + 18k = 21k.
S = (1/2)*21 = 10,5 кв.ед.
2 Чтобы найти широту, используйте горизонтальные линии, начерченные на карте – параллели. Определите, на какой параллели находится ваша точка, и найдите ее значение в градусах. Около каждой горизонтальной параллели есть обозначение в градусах (слева и справа). Если точка расположена прямо на ней, смело делайте вывод о том, что ее широта равна этому значению.
3 Если же выбранное место лежит между двумя параллелями, указанными на карте, определите широту ближайшей к нему параллели и прибавьте к ней длину дуги в градусах до точки. Длину дуги посчитайте при транспортира или примерно, на глаз. Например, если точка посередине между параллелями 30º и 35º, то ее широта будет равна 32,5º. Поставьте обозначение N, если точка расположена над экватором (северная широта) и обозначение S, если она находится под экватором (южная широта).
4 Определить долготу вам меридианы – вертикальные линии на карте. Найдите меридиан, ближе всего расположенный на карте к вашей точке и посмотрите его координаты, указанные сверху и снизу (в градусах). Измерьте с транспортира или прикиньте на глаз длину дуги между этим меридианом и выбранным местом. Прибавьте полученное расстояние в градусах к найденному значению долготы и получите долготу искомой точки.