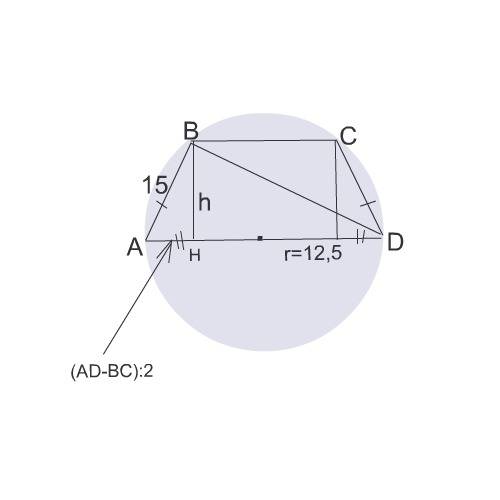
Дана трапеция АВСD, вокруг которой описана окружность.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Из этого следует, что трапеция равнобедренная.
АВ=СD=15 см
Площадь трапеции равна произведению ее высоты на полусумму оснований.
Известно только одно основание - оно равно диаметру окружности
АD=2 r=25 cм
Так как центр описанной окружности лежит на большем основании трапеции,
диаметр окружности, ее боковая сторона и диагональ образуют прямоугольный треугольник с гипотенузой, равной диаметру.
Высоту трапеции h = ВD найдем по формуле высоты прямоугольного треугольника, проведенного из прямого угла к гипотенузе:
h = 2s/a , где а - гипотенуза.
Площадь треугольника пока не известна.
Для ее нахождения нужно найти длину второго катета -диагонали трапеции ВD.
ВD=√(АD²-АВ²)=√(25²-15²)=√400=20 см
2s ABD=АВ·ВD=15·20=300 cм²
h =300:25= 12 см
Отрезок от А до основания Н высоты ВН трапеции равен в равнобедренной трапеции полуразности оснований.
АН найдем из прямоугольного треугольника АВН по теореме Пифагора.
Полуразность оснований 9 см
Разность оснований 18 см
Меньшее основание
ВС= 25 -18=7 см
S трапеции = 12·(25+7):2 =192 см²
80
Объяснение:
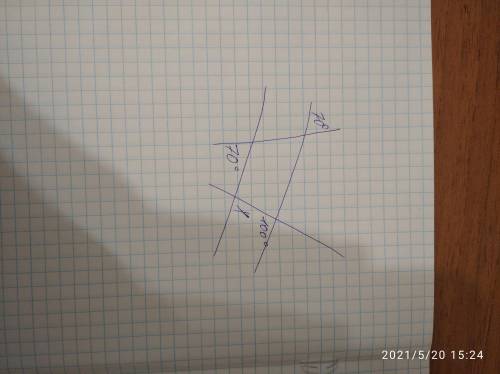
Так как самый нижний правый у левой палочки угол у тебя 70°, то вертикальный угол равен 70.
равен 70.
Так как самый верхний левый угол у левой палочки равен 70, то его вертикальный угол равен тоже 70.
Найденные нами углы являются внутренними разносторонними , а их равенство доказывает то, что прямые, относительно которых найденные углы внутренние разносторонние, параллельными*.
, а их равенство доказывает то, что прямые, относительно которых найденные углы внутренние разносторонние, параллельными*.
Учитывая это мы спокойно можем сказать, что сумма двух внутренних односторонних углов равна 180.
углов равна 180.
⇒ 100 + х = 180
х = 80
--------------------------------------------------------------------------------------------------------------
1.вертикальные углы - Углы, у которых вершина общая и стороны которых продолжают друг друга, называются вертикальными углами (рис. 1).
На приведенном рисунке вертикальными есть углы AOB и COD, а также AOC и BOD .
Вертикальные углы образуются при пересечении двух прямых.
2,3. Свойства углов, образованных при пересечении параллельных прямых секущей:
Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами. Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами. Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
При пересечении прямых секущей образуются такие пары углов:
Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами. Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами. Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.Запомните признак параллельности прямых:
Если при пересечении двух прямых секущей внутренние разносторонние углы равны или сумма внутренних односторонних углов равна 180 градусам, то заданные прямые параллельны.
Запомните последствия признаки параллельности прямых:
Две прямые, перпендикулярные к третьей, параллельны между собой. Прямые параллельны, если при их пересечении секущей образованы соответствующие углы равны.При пересечении двух параллельных прямых секущей образуются углы, которые имеют такие свойства:
Внутренние разносторонние углы при параллельных прямых и секущей уровне. Сумма двух внутренних односторонних углов при параллельных прямых и секущей равна 180 градусам. Две соответствующие углы при параллельных прямых и секущей уровне.Обратите внимание! Если прямая перпендикулярна одной параллельной прямой, то она перпендикулярна и другой.