1. В окружности с центром в точке O к хорде AB, равной радиусу окружности, перпендикулярно проведен диаметр CD. Диаметр CD и хорда AB пересекаются в точке Т. Длина отрезка AT равна 7 см. А) Постройте рисунок по условиям задачи;
Б) Определите длину хорды AB;
С) Определите длину диаметра CD;
Д) найдите периметр треугольника OAB.
2. В прямоугольном треугольнике ACB(Угол С=90°) AB = 16, угол ABC = 30°. С центром в точке А проведена окружность. Каким должен быть ее радиус, чтобы:
а) Окружность касалась прямой;
b) Окружность не имела общих точек с прямой BC;
с) Окружность имела две общие точки с прямой BC?
3. Постройте треугольник ABC по следующим данным:
AB = 4 см. BC = 3 см. Угол B=60°. В полученном треугольнике постройте биссектрису угла C.
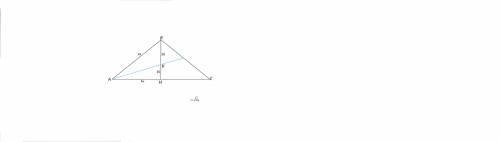
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см