Докажите что треугольнике pkf равнобедренный, если km = ke, mf = ef, точки M и E лежат на стороне pf

👇

Увидеть ответ

Открыть все ответы

Ответ:

EkaterinaTrenina

15.02.2021

Нет

Объяснение:

Рассмотрим белый (незаполненный) прямоугольный треугольник.

Мы знаем длину большего катета (=ребру куба=a) и прилежащий угол = 30°. Следовательно, второй острый угол =180-90-30=60°.

Найдём длину второго катета b:

гипотенуза с=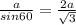 $\frac{a}{sin60}=\frac{2a}{\sqrt{3} }$ ,

$b=c*cos60=\frac{2a}{\sqrt{3} }*\frac{1}{2}=\frac{a}{\sqrt{3} }.$

Определим площадь треугольника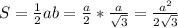 $S=\frac{1}{2}ab=\frac{a}{2}*\frac{a}{\sqrt{3} }=\frac{a^{2} }{2\sqrt{3} }$ .

Значит, объём, который останется незаполненным, равен объёму призмы с рассматриваемым нами треугольником в основании:

V(незаполненный)=Vпризмы=SΔ×a=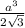 $\frac{a^{3} }{2\sqrt{3} }$ .

Объём максимально доступный нам для наполнения логично равен Vmax=V(куба)-V(незаполненный)=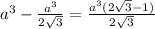 $a^{3}-\frac{a^{3}}{2\sqrt{3}}=\frac{a^{3}(2\sqrt{3}-1)}{2\sqrt{3}}$ .

Наконец, найдём отношение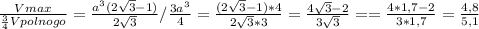 $\frac{Vmax}{\frac{3}{4}Vpolnogo }=\frac{a^{3}(2\sqrt{3}-1)}{2\sqrt{3}}/\frac{3a^{3}}{4}=\frac{(2\sqrt{3}-1)*4 }{2\sqrt{3}*3}=\frac{4\sqrt{3}-2}{3\sqrt{3}}==\frac{4*1,7-2}{3*1,7}=\frac{4,8}{5,1}$ <1, следовательно Vmax< 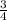$\frac{3}{4}$ Vполного, т.е. наполнить сосуд водой на три четверти не получится.

4,4(19 оценок)

Ответ:

svr2

15.02.2021

Дано:
на картинке

Решение:
Так как пирамида правильная и SO перпендикулярно ABCD, то SOA - прямоугольный треугольник. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов равен половине гипотенузы. Значит SO=SA/2.

Обозначим SA=2a, тогда SO=a. По теореме Пифагора найдем ОА:
$OA= \sqrt{SA^2-SO^2}= \sqrt{(2a)^2-a^2}= a \sqrt{3}$

Так как в основании лежат квадрат, то он имеет равные взаимно перпендикулярные диагонали, которые точкой пересечений делятся пополам. Значит, треугольник АВО - прямоугольный и АО=ВО.
По теореме Пифагора находит АВ из прямоугольного треугольника АВО:
$AB= \sqrt{AO^2+BO^2}= \sqrt{(a \sqrt{3} )^2+(a \sqrt{3} )^2}= a\sqrt{6}$

Так как точка Н - середина АВ, то НВ=НА=АВ/2
Из прямоугольного треугольника OНВ находим OН по теореме Пифагора:
$OH= \sqrt{BO^2-HB^2} = \sqrt{AO^2-HB^2} =
\\\
=\sqrt{(a \sqrt{3}) ^2-( \frac{a \sqrt{6} }{2})^2} =a\sqrt{( \sqrt{3}) ^2-( \frac{ \sqrt{6} }{2})^2} =a\sqrt{3- \frac{6 }{4}} =a\sqrt{ \frac{6 }{4}} = \frac{a \sqrt{6} }{2}$

Из прямоугольного треугольника SOH:
$tgSOH= \frac{SO}{OH} =a: \frac{a \sqrt{6} }{2} = \frac{2}{ \sqrt{6} } =\frac{2\cdot \sqrt{6}}{ \sqrt{6}\cdot \sqrt{6} } =\frac{2\sqrt{6}}{6 } =\frac{\sqrt{6}}{3 } \\\ \Rightarrow SOH=\mathrm{arctg} \frac{\sqrt{6}}{3 }$

ответ: $\mathrm{arctg} \frac{\sqrt{6}}{3 }$
Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые