Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 2√3, а периметр равен 3(1+ √3).
Дано: ∠C =90° , P =a+b+c = 3(1 + √3) ,где а и b _катеты , c = 2√3 (гипотенуза).
- - - - -
∠A - ? , ∠B - ?
" решение " : пусть ∠A = α ⇒ a =c*sinα , b =c*cosα
* * * очевидно: sinα > 0 ; cosα > 0 * * *
c*sinα + c*cosα + c = 3(1 + √3) || c =2√3 | ⇔
2√3 (sinα + cosα) +2√3 =3(1 + √3) ⇔2√3( sinα + cosα) = √3 + 3 ⇔
2√3(sinα + cosα ) =√3( 1 +√3) ⇔ sinα + cosα =(1 +√3 ) /2 ⇔
(sinα + cosα)² = ( (1 +√3 ) /2 )² ⇔sin²α + cos²α+2sinα*cosα = 1 +(√3 ) /2 ⇔
1 +sin2α = 1 +(√3) /2 ⇔ sin2α = (√3) /2 ⇒ 2α = 60° или 2α = 120°
α = 30° или α = 60°
∠A = α = 30° ; ∠B = 90° - ∠A = 90° - 30° = 60°
или α = 60°
∠A = α = 60° ; ∠B = 90° - ∠A = 90° - 60° = 30°
ответ : ∠A = 30° ; ∠B = 60° или наоборот ∠A = 60° ; ∠B = 30° .
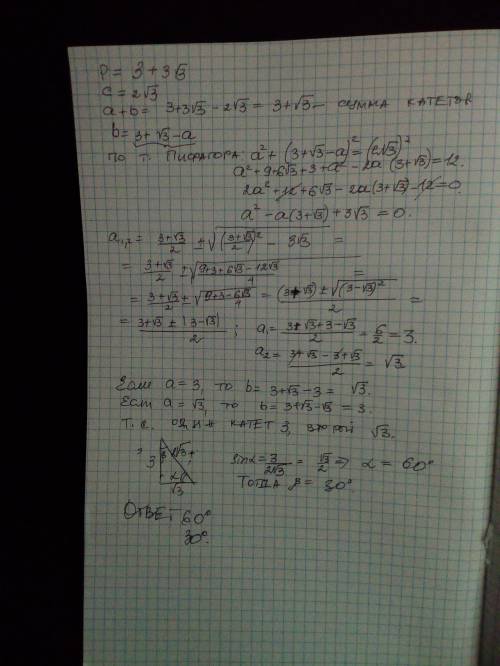
ответ: Р = 240 см.
Объяснение:
Рассмотрим 4-угольник ANCM:
Угол NCM = 360 - угол MAN - 90 - 90 (так как AN,AM - высоты) = 360 - 180 - 60 = 120 градусов, причём по свойствам ромба угол NCM равен углу BAD.
Теперь рассмотрим сам ромб. Так как его тупые углы нам известны, то можно найти острые углы:
Угол ADC равен углу ABC и равен (360 - 120 -120)/2 = 120/2 = 60 градусов.
Рассмотрим треугольник ADM. Он прямоугольный с углом AMD = 90 градусов (АМ - высота). Найдём угол DAM:
Угол DAM равен (180 - 90 - угол ADM) = (90 - угол ADC) = (90 - 60) = 30 градусов. Катет против угла в 30 градусов равен половине гипотенузы, то есть DM = 1/2 AD => AD = 2DM = 2 * 30 = 60 см.
Так как в ромбе все стороны равны, то Рромба = 4 * AD = 4 * 60 = 240 см.