Объяснение:
сколько квадратных метров листовой жести пойдет на изготовление бака в форме усеченного конуса глубиной 96 см и радиусами оснований 68 см и 40 см, если на швы необходимо добавить 2% площади полной поверхности
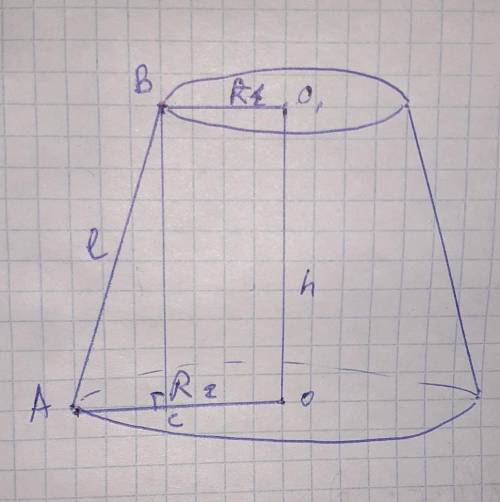
R1=40см
R2=68см
h=96см
Sпол×2%
найти
Sж - ?
Площадь полной поверхности усеченного конуса складывается из суммы площадей основании и площади боковой поверхности
Sполн= πR1²+ π(R1+R2)×L + R2²= π(R1²+(R1+R2)L+R2²
чтобы найти площадь боковой поверхности надо вычислить длину образующей L.
Образующую находим по теореме Пифагора.
Имеем прямоугольный треугольник ΔABC
где гипотенуза = образующей АB=L
катет= высота конуса ВС=h =96см
второй катет АС=АО-СО=R2-R1=68-40=28см
R1=BO1=40см
R2=AO=68см
ВО1=СО=40см
образующая L=AB
AB=√AC²+BC²=√28²+96²=√784+9216=√10000=100 см
AB=L=100см
площадь полной поверхности усеченного конуса
Sполн=π(40² + (40+68)×100 + 68²)= π(1600+10800+4624)=
=17024π см²
или если умножить на число π
Sполн = 17024×π=17024×3,14=53455,36 см²
площадь жести потраченное на изготовление бака
Sж= Sпол×2% + Sпол=17024π×2% + 17024π=
=340,48π+17024π=17364,48π см²
или
S ж=17364,48×π=17364,48×3,14= 54524,4672 см²
ответ: 1/2
Объяснение:
1. Имеем 2 круга
1-ый с радиусом R=O1B =1
2-ой с радиусом OO1=OA=OB и диаметром AB.
Рассмотрим второй круг и найдем его радиус:
Треугольник АО1В прямоугольный и равнобедренный ( так как АО1=О1В=R)
Тогда АВ = О1В*sqrt(2)= sqrt(2)
OA=AB/2=r =sqrt(2)/2
Найдем площадь круга с радиусом r
S(r)= pi*r^2=pi*(sqrt(2)/2)^2=2*pi/4= pi/2
Найдем площадь четверти круга радиуса R
S(R)/4=pi*R^2/4=pi*1/4=pi/4
Тогда площадь выделенной части + площадь двух сегметов слева оси О1А и ниже оси О1В равна S(r)-S(R)/4= pi/2-pi/4=pi/4
Найдем площади указанных сегментов:
Поскольку треугольник АО1В равнобедренный, то его площадь
S(AO1B)= O1B^2/2= R^2/2=1/2
Площадь половины круга радиуса r = S(r)/2= pi/2/2= pi/4
Сумма площадей обоих сегментов равна
Ssegm= S(r)/2- S(AO1B)= pi/4-1/2
Тогда площадь выделенной фигуры равна
pi/4- (pi/4-1/2)= pi/4-pi/4+1/2=1/2