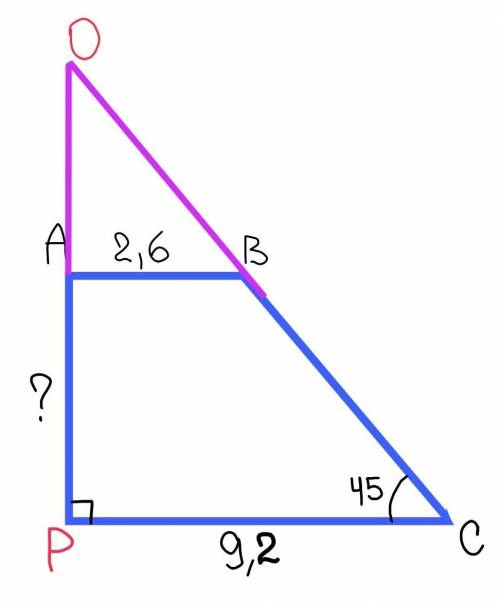
Продлим РА за точку А и СВ за точку В, точку пересечения назовём О.
∆РОС – прямоугольный с прямым углом Р.
Сумма острых углов прямоугольного треугольника равна 90°. Исходя из этого: угол РОС=90°–угол ОСР=90°–45°=45°.
Получим что угол РОС=угол ОСР, тогда ∆РОС – равнобедренный с основанием ОВ.
Тогда РО=РС=9,2 см.
Основания трапеции параллельны, тоесть АВ//РС.
Следовательно: угол ОВА=угол ОСР как соответственные при параллельных прямых АВ и РС и секущей ОС; тогда угол ОВА=45°.
Угол АОВ=45° (доказано ранее)
Получим что угол ОВА=угол АОВ.
Тогда ∆АОВ – равнобедренный с основанием ОВ. Следовательно АО=АВ=2,6 см.
РА=РО–АО=9,2–2,6=6,6 см.
ответ: 6,6 см.
Проводим линию параллельную меньшей боковой стороне трапеции от угла, который между меньшим основанием и большей боковой стороной трапеции. Мы получаем прямоугольный треугольник, два угла которого равны 45 и 90 градусам.
Следующий шаг - отнимаем от большего основания меньшее - 10,7-2=8,7 (см) - длина большего основания за линией или один из катетов угла.
Так как сумма углов треугольника равна 180 градусам, то находим оставшийся угол этого самого треугольника - 180-90-45=45 градусов.
Угол в 45 градусов равен второму углу в 45 градусом, следовательно, этот треугольник - равнобедренный и его второй катет равен 8,7 см.
Так как второй катет проведен параллельно меньшей боковой стороне, то они, соответственно, равны 8,7 см.
ответ 8,7 см
Касательные имеют теорему: радиус, проведённый с точки касания до центра окружности — перпендикулярен её касательной.
То есть: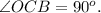
Так что, треугольники COB & OAB — прямоугольные.
Нам известна гипотенуза OB, равна 24см, и катет CB — равный 12см.
Что-что!?, что мы замечаем? Гипотенуза OB в 2 раза больше катета CB?
Правильно:
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Теорема действует и в обратном порядке: Если катет равен половине гипотенузы, то ему прилежащий угол равен 30°, что и означает, что:
Теорема о 2 касательных, проведённых с одной точки таков: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
Значит OB — биссектриса, что и означает, что <B = 30*2 = 60°.
Вывод: угол между касательными равен 60°.