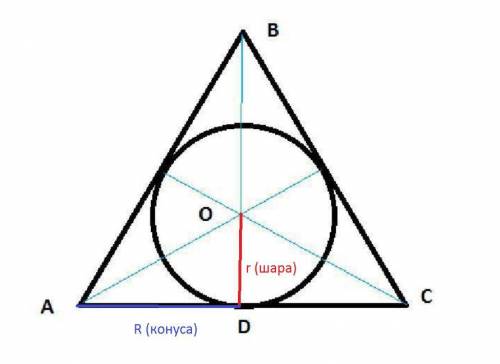
Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, РВСМ=РМDР - накрестлежащие, РВМС=РDМР - вертикальные) , поэтому ВМ=МР или точка М - середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
КМ = 1/2АР=1/2(АD+DF)=1/2(AD+BC)
рисунок не забудь,