Объяснение:
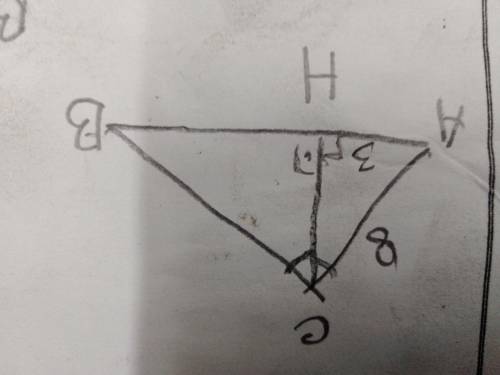
∆ABC ~ ∆ACN как ∆ образованные взаимно перпендикулярными сторонами, СН=АС^2 - АН^2
СН= √(8^2-3^3)=√(8-3)(8+3)=√55
АН : АС = АС : АВ
АВ= АС^2/АН;. АВ=8^2/3=64/3
найдем ВС по т. Пифагора,
ВС=√(АВ^2 - АС^2)= √((64/3)^2-8^2)
ВС=1/3*√(56*72)=8√7
АВ=64/3,
ВС=8√7,
СН=√55
Объяснение:
Уравнение окружности имеет вид:
(x-x0)²+(y-y0)²=r²
Где (х0;у0) - координаты центра. r- радиус.
Подставив вместо х и у координаты данных точек получаем систему трех уравнений с тремя неизвестными:
для упрощения записи, вместо х0 напишу х, а вместо у0 напишу у:
(-3-x)²+y²=r²
(1-x)²+(3-y)²=r²
(5-x)²+y²=r²
вычтем из первого уравнения третье:
(-3-x)²-(5-x)²=0
9+6x+x²=25-10x+x²
16x=16
x=1
тогда получаем :
16+y²=r²
(3-y)²=r²
16+y²-(3-y)²=0
16+y²=9-6y+y²
6y=-7
y=-7/6
Тогда r²=820/49
Итак уравнение окружности имеет вид:
(x-1)²+(y+7/6)²=820/49
ответ:не знаю как точно вы решаете но вот решение
Объяснение:
1-рассмотрим треугольники абс и адс. т.к. ад равно аб и и угол дас равен углу бас (по усл) то ас- общая стоона следовательно треугольники равны по трем сторонам, а т.к. треугольники равно то их стороны будут равны. следовательно бсравно дс 2-т.к. ас и дс равны (как диагонали трапеции) следовательно это равнобедренная трапеция. у равнобедренной трапеции 2 стороны равны то следовательно да равно сб3- т.к. абсд это параллелограмм и ДА равно СБ по условию, то следовательно их диагонали будут равны. ас и бд и есть диагонали . следовательно они равны
АВ=21цел1/3см
СВ=8√55/3 см
СН=√55 см
Объяснение:
Теорема Пифагора
СН=√(АС²-АН²)=√(8²-3²)=√(64-9)=√55 см
СН²=АН*НВ
НВ=55/3=18цел1/3 см
АВ=АН+НВ=3+55/3=9/3+55/3=64/3=
=21цел1/3
СВ=√(НВ*АВ)=√(55/3*64/3)=8√55/3 см