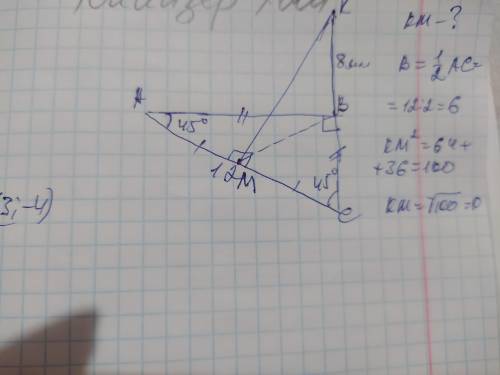
ответ: КМ=10см
Объяснение: обозначим расстояние отрезок от точки К до прямой АС- КМ. Проэкция КМ на плоскость АВС- это ВМ. ∆АВС- равнобедренный, так как сумма острых углов прямоугольного треугольника составляет 90°, поэтому угол В=90-45=45°. Углы треугольника при основании равны, поэтому АВ=ВС. Проэкция ВМ тогда является медианой, и поскольку медиана проведённая из вершины прямого угла равна половине гипотенузы, то ВМ=½× АС=12/2=6см. Проэкция ВМ, перпендикуляр ВК и КМ образуют прямоугольный треугольник с катета и ВК и ВМ, а КМ - гипотенуза. Найдём её по теореме Пифагора:
КМ²=ВК²+ВМ²=8²+6²=64+36=100;
КМ=√100=10см
Даны середины сторон треугольника АВС с координатами К(-2;2), L(0;7), М(4;-1).
Треугольник KLM подобен АВС с к = 1/2. Поэтому площадь АВС равна четырём площадям треугольника KLM.
Можно по разности координат точек найти длины сторон треугольника KLM, затем по формуле Герона найти площадь KLM.
Но можно поступить проще: есть простая формула определения площади треугольника по координатам вершин.
Площадь треугольника KLM равна:
S =(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)|.
Подставив координаты точек, находим: S(KLM) = 18 кв.ед.
Отсюда ответ: S(АВС) = 18*4 = 72 кв.ед.
<АВС=70°
Объяснение:
ДугаАС=140°
<АОС=140° центральный угол опирается на дугуАС.
<АВС=<АОС:2=140°:2=70° вписанный угол опирается на дугуАС.