
В прямоугольном равнобедренном треугольнике угол между катетом и гипотенузой равен 45 градусов. Тангенс равен 1.
Используем формулу угла между прямыми по угловым коэффициентам.
Угловой коэффициент заданной прямой равен k₁ = (-2/3).
tg φ = (k₂ - k₁/(1 + k₁*k₂). Приравняем тангенс 1.
1 +(-2/3)*k₂ = k₂ - (-2/3),
(5/2)k₂ = 1/3,
k₂ = 1/5.
Уравнение катета СА имеет вид у = (1/5)х + в.
Для определения параметра в подставим координаты точки С(2; -1).
-1 = (1/5)*2 + в,
в = -1 - (2/5) = -7/5.
Получаем уравнение катета СА: у = (1/5)х - (7/5).
Угловой коэффициент катета СВ k₃ = -1/k₂ = -1/(1/5) = -5.
Уравнение катета СВ имеет вид у = (-5)х + в.
Для определения параметра в подставим координаты точки С(2; -1).
-1 = (-5)*2 + в,
в = -1 + 10 = 9
Уравнение катета :СВ у = (-5)х + 9.
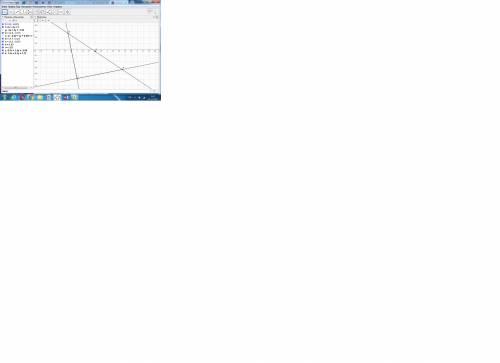
Радиус окружности вписанной в квадрат равна 3√2см. Найти сторону квадрата и радиус окружности, описанной около квадрата.
Объяснение:
1) Тк окружность вписана , то она касается всех сторон квадрата и диаметр окружности равен стороне квадрата : а₄=2r=2*3√2=6√2 (cм).
2) Если теперь около квадрата ABCD описать окружность, то диагональ квадрата AC равна диаметру окружности .
ΔАВС-прямоугольного , по т. Пифагора АС=√( (6√2)²+(6√2)²)=12 (см).
Поэтому радиус , описанной около квадрата , окружности R=12:2=6 (см).
Все снизу
Объяснение:
1. 0.2*0.7=0.14
0.14/0.42=
2. Сначала перенесем 18 влево и получим x²+3x-18=0
По теореме Виета
x₁+x₂= -3
x₁*x₂= -18
x₁= -6
x₂= 3
3. По формуле S=1/2d₁d₂
S=1/2*10*6=5*6=30cм²
4. Достроим BK перпендикулярно ОА, по клеточкам посчитав получим что:
BK=6cм
OK=2cм
tg=6/2=3см
5. Самая большая высота=5см