Sосн=36см²
Sбок=224см²
Sпол=296см²
V=288cм³
Объяснение:
Дано
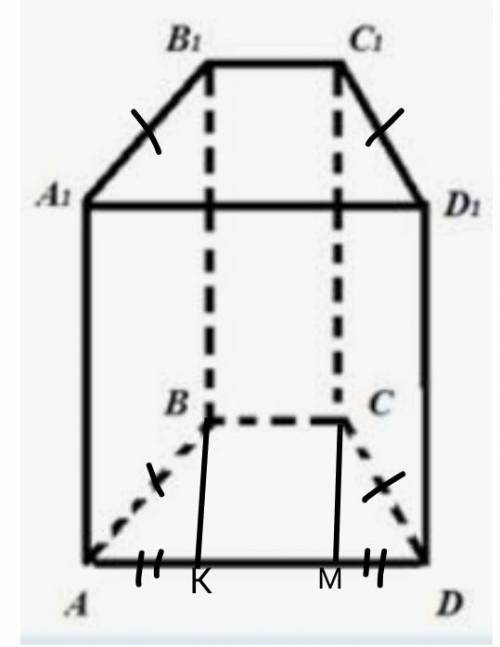
ABCDA1B1C1D1- призма
ABCD- трапеция
АВ=CD=5см боковая сторона трапеции.
ВС=6см верхнее основание трапеции.
АD=12см нижнее основание трапеции.
В1В:ВК=2:1.
Sосн.=?
Sбок=?
Sпол=?
V=?
Решение.
АК=МD
AK=(AD-BC)/2=(12-6)/2=6/2=3 см.
∆АВК- прямоугольный (<ВКА=90°)
По теореме Пифагора найдем высоту трапеции.
ВК²=АВ²-АК²=5²-3²=25-9=16см.
ВК=√16=4 см высота трапеции.
Sосн=ВК(ВС+AD)/2=4*(6+12)/2=4*18/2=
=36см² площадь трапеции.
ВВ1=2*ВК=2*4=8см высота призмы.
Росн=АВ*2+ВС+AD=5*2+6+12=10+18=28см периметр трапеции.
Sбок=Росн*ВВ1=28*8=224см² площадь боковой поверхности призмы.
Sпол=2Sосн+Sбок=2*36+224=72+224=
=296 см² площадь полной поверхности призмы.
V=Sосн*ВВ1=36*8=288см³ объем призмы.
AOD - прямоугольный треугольник.
ОР - высота из прямого угла в треугольнике AOD.
ОР=√(АР*РD)=√(6√3*2√3)=6см.
По Пифагору АО=√(АР²+ОР²)=√(108+36)=12см.
R=AJ=JO=JP = АО/2 = 6см.
Площадь круга Sк=π*R²=36π.
В прямоугольном треугольнике АРО катет ОР равен половине
гипотенузы АО, значит <PAO=30°,
<РАК=60° (так как АО - биссектриса <PAK) => дуга РОК=120°.
<PJK=120°(центральный угол, опирающийся на дугу РОК).
РН=0,5*АР=3√3см (катет против угла 30°).
AH=√(АР²-РH²)=√(108-27)=9см.
Площадь треугольника АКР равна
Sapk=AH*PH=9*3√3=27√3см².
Площадь сегмента КОР равна
Skop=(R²/2)*(π*α/180 -Sinα) - формула.
В нашем случае α=<PKJ =120°.
Skop=(36/2)*(π*120/180 -√3/2)
Skop=(12π-9√3)см².
Искомая площадь равна
S=Sк-Sapk-Skop = 36π-27√3-12π+9√3 = (24π-18√3)см².