Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

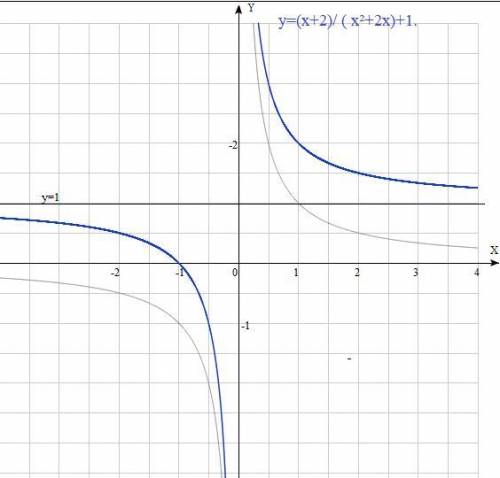
Построить график функции у=(х+2)/ ( х²+2х)+1. Указать значения m , при котором прямая у=m имеет с графиком общие точки.
Объяснение:
у=(х+2)/ ( х²+2х)+1 , область определения функции х²+2х≠0
или х(х+2)≠0 или х≠0 , х≠-2.
После сокращения на (х+2) получаем :
у=1/х+1 , при х≠0 , х≠-2. Это гипербола полученная сдвигом графика функции у=1/х по оси оу на 1 единицу вверх.
Таблица значений для у=1/х :
х...-2........-1......-0,5.....0,5.....1......2
у...-0,5....-1......-2.........2.........1.....0,5
Затем каждую точки сдвигаем вверх на 1 , получаем график функции у=(х+2)/ ( х²+2х)+1 ( на чертеже синий)
При m∈(-∞;1)∪(1;+∞) прямая у=m имеет с графиком общие точки.