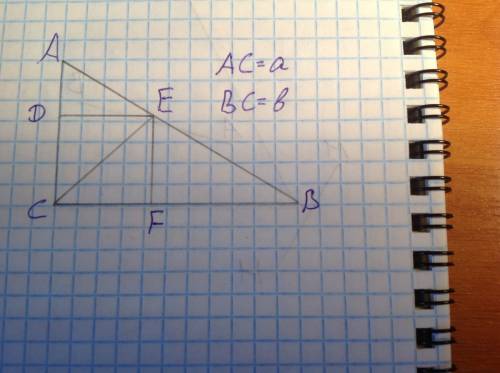Вравнобедренной трапеции острый угол равен 60°.докажите,что основание равно разности большего основания и боковой стороны.

👇

Ответ:

buckubarnes17

02.01.2022

Опустим из вершин меньшего основания перпендикуляры к большему. Трапеция равнобедренная, значит, большее основание равно меньшему основанию плюс два равных отрезка при углах 60°.Отрезки находим из прямоугоных треугольников, в которых один из углов по условию задачи 60°, второй по построению 90°, третий, соответственно, 30°.Известно, что катет, противолежащий углу 30°, равен половине гипотенузы. Величина отрезков АН и КД равна 16:2=8 смАД=8*2+хАД+ВС=16+х+х=38см2х=22смх=11 см-это меньшее основаниех+16=27 см- это большее основание.ответ: АД=27 см,ВС=11 см

4,4(21 оценок)

Открыть все ответы

Ответ:

Алиналабвдк

02.01.2022

соединим концы хорд

получим четырехугольник

так как хорды параллельные - это вписанная равнобедренная трапеция

обозначим

R - радиус описанной окружности

c - боковая сторона трапеции

h = 42 высота трапеции

a = 36 и b = 48 - Основания

диагонали трапеции равны по теореме Пифагора

d^2 = h^2 + (a+(b-a)/2)^2 = 42^2 +(36 +(48-36)/2)^2 =3528

d = 42√2

боковая сторона

с^2 = h^2 + ((b-a)/2)^2 =42^2 +((48-36)/2)^2=1800

c = 30√2

диагональ(d), нижнее основание(b) и боковая сторона(c) образуют

треугольник , вершины которого лежат на той же описанной окружности

периметр треугольника P = b+c+d = 48+30√2+42√2=48+72√2

полупериметр треугольника p = 24+36√2

тогда радиус описанной окружности по известной формуле

R = (bcd) / 4√(p(p-b)(p-c)(p-d))=

=(48*30√2*42√2) / 4√((24+36√2)(24+36√2-48)(24+36√2-30√2)(24+36√2-42√2))= 30

ответ R=30

4,8(48 оценок)

Ответ:

Monika950

02.01.2022

Пусть в прямоугольный треугольник ABC вписан квадрат CDEF (см. рисунок). Здесь AC=a, BC=b.
Заметим, что диагональ CE квадрата является также биссектрисой исходного треугольника. Пусть CE=d, тогда CD=d√2/2 - сторона квадрата меньше диагонали в √2 раз. Периметр квадрата равен (d√2/2)*4=2√2d, а площадь равна (d√2/2)²=d²/2. Таким образом, чтобы найти периметр и площадь квадрата, достаточно выразить биссектрису прямого угла d через a и b.

Площадь прямоугольного треугольника равна половине произведения катетов, в нашем случае S=ab/2. Теперь воспользуемся другой формулой площади - S=1/2*a*b*sin(C), где a,b - соседние стороны треугольника, а sin(C) - угол между ними. Тогда S(ACE)=1/2*AC*CE*sin(45), S(BCE)=1/2*CE*BC*sin(45) (углы ACE и BCE равны 45 градусам). Так как S(ACE)+S(BCE)=S(ABC), мы можем записать уравнение с одним неизвестным CE:
1/2*AC*CE*sin(45)+1/2*CE*BC*sin(45)=ab/2
AC*CE*sin(45)+CE*BC*sin(45)=ab
CE(AC+BC)=ab/sin(45)
CE=ab/(a+b)sin(45)
Таким образом, d=ab/(a+b)sin(45). Получаем, что периметр квадрата равен 2√2d=2√2ab/(a+b)sin(45)=4ab/(a+b), а площадь равна d²/2=(ab/(a+b)sin(45))²*1/2=a²b²/(a+b)².
Впрямоугольный треугольник с катетами a и b вписан квадрат имеющий с треугольником общий прямой угол