Бери циркуль, линейку, карандаш, строй сначала квадрат, будем его крутить. Пусть квадрат называется незатейливо АВСД, крутить будем относительно вершины А. 1. Ставишь циркуль иголкой в вершину А, вторую ножку циркуля совмещаешь с точкой В. Проводишь окружность радиуса АВ с центром в А. 2. Иголку циркуля переносишь в точку В, и не изменяя раствор циркуля, делаешь на окружности в направлении вращения засечку. 3. Переносишь иголку циркуля на засечку, и продолжая в том же направлении, делаешь на окружности вторую засечку. Это будет точка В1 - новая вершина повёрнутого квадрата. 4. Далее шаги 2 и 3 повторяешь для точки Д, и таким же образом делаешь первую засечку, и вторую засечку. Два шага по окружности. Второй шаг даст тебе точку Д1 - новую вершину повёрнутого квадрата. 5. Возвращаешь иголку циркуля в точку центра вращения А. Строишь окружность (на самом деле будет достаточно половины окружности в направлении вращения) радиусом как диагональ квадрата, то есть АС. 6. Таким же образом делаешь последовательно две засечки, и вторая даст тебе точку С1 - новую точку повёрнутого квадрата. 7. Соединяешь последовательно точки А В1 С1 Д1, и получаешь повёрнутый квадрат. Если всё сделано аккуратно, без болтанки циркулем и тремора рук, то картинка получится вполне красивая.
Объяснение:
1.
В любом треугольнике — сумма двух сторон должна быть больше оставшийся стороны, тоесть предположми, что боковые друг другу равны стороны — 7.49; 7.49, а основание — 3.74.
7.49+7.49 = 14.98 > 3.74 (сумма двух сторон больше)
3.74+7.49 = 11.23 > 7.49 (сумма двух сторон больше)
7.49+3.74 = 11.23 > 7.49.
Как мы видим, сумма каждых двух сторон больше каждой оставшийся стороны, тоесть — такой треугольник существует.
Вариант 2: боковые стороны — 3.74, основание — 7.49.
3.74+3.74 = 7.48 < 7.49.
Как мы видим сумма двух боковых сторон меньше основания, что и означает, что треугольник с боковыми сторонами 3.74; 3.74, и основанием — 7.49 — существовать не может.
2.
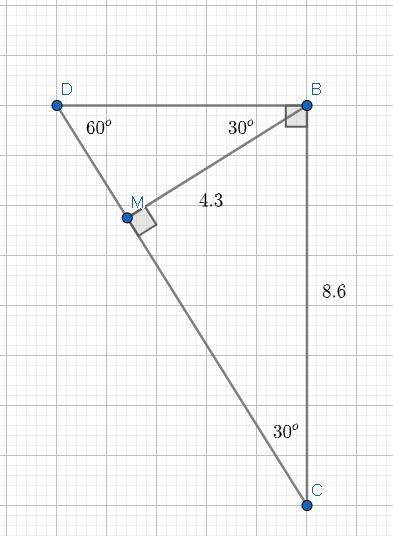
Треугольник MBC — прямоугольный треугольник, так как высота(или катет) обрзует прямой угол <BMC.
BC = 8.6; <C = 90-60 = 30° ⇒ MB = BC/2 (теорема о 30-градусном угле прямоугольного треугольника).
MB = BC/2 ⇒ MB = 8.6/2 = 4.3.
Вывод: Высота MB равна 4.3.
Квадрат стороны тр-ка равен: с² = а²+в² -2*а*в*CosC.(по теореме косинусов)
В нашем случае с² = 89 - 80*Cos126,7° = 89 - 80*(- 0,6) = 89+47,8=136,8
Тогда искомая сторона АВ =с = 11,69см