Прямые заданы уравнениями 3х+2у-9=0, у+3=0 а) начертите эти прямые в одной системе координат б) найдите координаты точки пересечения этих прямых в) найдите площадь треугольника, образованными этими прямыми и осью ординат.

👇

Увидеть ответ

Ответ:

надюша5056

09.11.2021

а) Выразим у через х.

3х + 2у - 9 = 0, у + 3 = 0

у = - 1,5х + 4,5 у = - 3 (1)

Для построения первой прямой возьмем два произвольных значения х и вычислим для них соответствующие значения у:

x = 1, y = - 1,5 + 4,5 = 3

x = 3, y = - 1,5 · 3 + 4,5 = 0

Через точки (1; 3) и (3; 0) проведем прямую.

Для построения второй прямой на координатной плоскости отметим точку у = -3 и начертим через эту точку прямую, параллельную оси Ох.

б) Приравняем правые части двух уравнений (1):

- 1,5х + 4,5 = - 3,

х = 5 - абсцисса точки пересечения.

Подставим это значение в уравнение прямой и найдем ординату точки пересечения:

у = - 1,5 · 5 + 4,5 = - 3.

Координаты точки пересечения равны (5; - 3).

в) Треугольник АВС, площадь которого нам нужно отыскать, прямоугольный,

АВ = 4,5 + 3 = 7,5

ВС = 5

Sabc = 1/2 AB · BC = 1/2 · 7,5 · 5 = 18,75 кв. ед.

4,4(37 оценок)

Открыть все ответы

Ответ:

lisa20060701

09.11.2021

Площадь ромба равна 120 см², а одна из диагоналей больше другой на 14 см. Найдите длину неизвестной диагонали.

▔ ▔ ▔

★☆★ Чертёж смотрите во вложении ★☆★

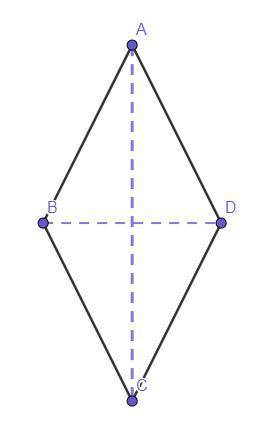
Дано:

Четырёхугольник ABCD — ромб.

S(ABCD) = 120 см².

AC и BD — диагонали.

АС = BD+14 см.

Найти:

BD = ?

Решение:

Пусть BD = х.

Тогда —

АС = х+14 см.

▸Площадь ромба равна половине произведения его диагоналей◂

То есть —

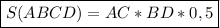
$\boxed {S(ABCD)=AC*BD*0,5}$

Подставим в формулу известные нам значения —

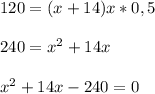
$120=(x+14)x*0,5\\\\240=x^{2}+14x\\\\x^{2}+14x-240=0$

Решаем полученное квадратное уравнение —

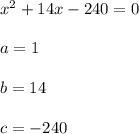
$x^{2}+14x-240=0\\\\a=1 \\\\b=14\\\\c=-240$

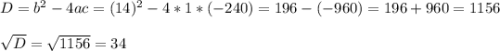
$D=b^{2} -4ac = (14)^{2} -4*1*(-240)=196-(-960)=196+960=1156\\\\\sqrt{D} =\sqrt{1156} =34$

Ищем корни —

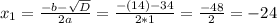
$x_{1} =\frac{-b-\sqrt{D} }{2a} =\frac{-(14)-34}{2*1} =\frac{-48}{2} =-24$

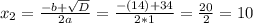
$x_{2} =\frac{-b+\sqrt{D} }{2a} =\frac{-(14)+34}{2*1} =\frac{20}{2} =10$

Как видим, корень х₁ не подходит, так как длина отрезка не может выражаться отрицательным числом.

Поэтому, BD = х = 10 см.

ответ:

10 см.

Площа ромба дорівнює 120 см а одна з діагональ більша за іншу на 14 см знайдіть іншу діагональ

4,6(70 оценок)

Ответ:

hodyukmaria

09.11.2021

У квадрата все стороны равны и его периметр составляет сумму длин всех четырех сторон или учетверенный размер одной стороны:

Р = а + а + а + а = 4 * а,

Где а - сторона квадрата.

То увеличение стороны квадрата на 25%, при условии, что фигура остается квадратом, влечет за собой увеличение всех сторон квадрата на 25% и значит, увеличивает периметр на длину одной стороны. Продемонстрируем.

Старая сторона квадрата составляла 100%, а новая составляет:

100% + 25% = 125%;

И равна:

b = а * 125 / 100 = 1,25 * а.

Новый периметр составит:

Рн = b + b + b + b = 4 * b = 4 * 1,25 а = 5 * а.

Найдем разницу периметров:

Рн - Р = 5 * а - 4 * а = а.

То есть разница между периметрами при увеличении стороны квадрата на 25% составляет длину одной стороны изначального квадрата.

4,5(10 оценок)

Это интересно:

Финансы-и-бизнес