2.
треугольникк это фигура которая состоит из трёх углов и трех прямых соединенных между собой в замкнутую цепь.треугольники бывают трех видов остроугольные тупоугольные и прямоугольные у остроугольных есть один угол как минимум который от 0 до 90 градусов у тупоугольного от 90 до 180 у прямоугольного есть хотя бы один угол 90 градусов по сторонам треугольники из трёх видов это равносторонние и равнобедренные и равносторонние разносторонний этого треугольника у которых длина сторон разные равнобедренная Когда две стороны равны между собой и равносторонние либо правильная треугольнике это те треугольники у которых все углы по 60 градусов и все стороны равны
3.
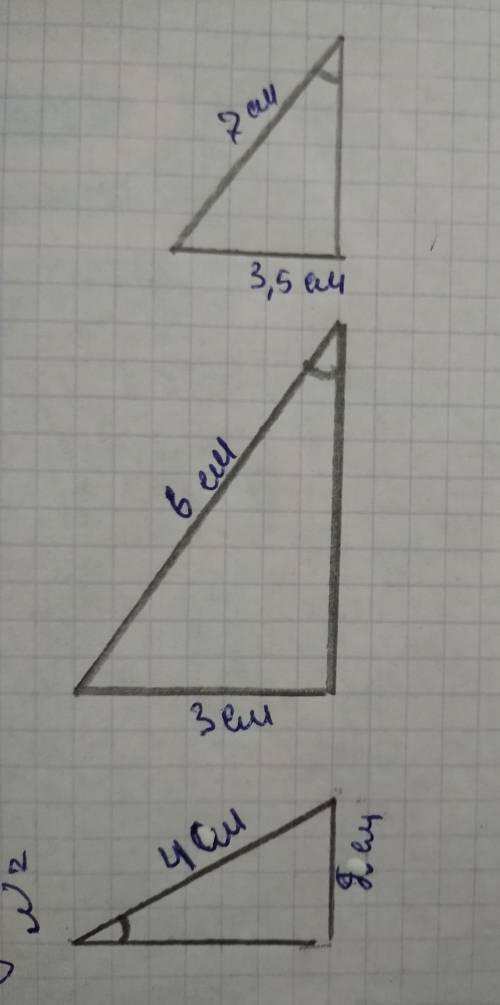
во всех треугольников будет сумма острых углов 90 градусов так как сумма всех углов треугольника 180 градусов и так как в прямоугольном треугольнике есть один угол 90 градусов то два других в сумме будут 180 - 90 равно 90.
номер 2
вывод: в каждом треугольнике есть угол 90 градусов и угол 30 градусов а значит что каждый острый угол будет равен 60 градусов так как сумма углов будет 180 градусов.длина катета зависит от гипотенузы и угла в 30 градусов.Катет лежащий против угла в 30 градусов равен половине гипотенузы. Дан треугольник у которого есть угол 90 градусов и 30 градусов То третье угол будет равен 60 так как сумма острых углов равна 90 и 90 - 30 равно 60 если Дан угол 30 градусов то второй угол равен 60 так как 90 минус 30 равно 60 - это тоже самое ссвойство.есть еще одно свойство про угол 30 градусов катет лежащий против угла в 30 градусов равен половине гипотенузы либо же наоборот половине гипотенузы равен катет лежащий против угла 30 градусов но 1 мне кажется легче.
остальное задание будет на фото

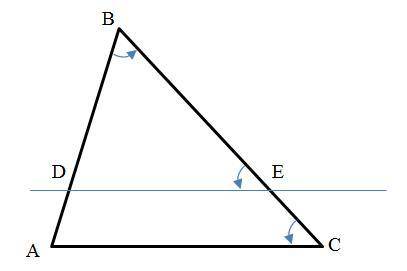
1-й признак подобия треугольников (подобие треугольников по двум углам). Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство.
На сторонах AB и BC треугольника ABC отметим точки D и E, соответственно (см. рисунок). Так как ∠BED = ∠BCA, то треугольники ABC и DBE подобны по первому признаку по углам B и ∠BED = ∠BCA.
У подобных треугольников все углы равны, то есть если для треугольников ABC и DBE имеет место ∠B = ∠B и ∠BED = ∠BCA, то ∠BDE = ∠BAC, что требовалось доказать.
Рассмотрим треугольник CKD. Он прямоугольный . Угол К равен 90 градусов , угол Д по условию 60 градусов, угол С 30градусов . Найдём КД. Он равен 10 см так как этот катет КД лежит напротив угла 30 градусов , то есть он равен половины гипотинузы. КД знаем , АД знаем можем найти АК.
АК равна БС . ОТ всего основания отнимаем отрезок кд и находим АК. ТО есть 20 - 10 равно 10 см , а как я уже говорил Ак равно БС , то это и есть размер меньшего основания