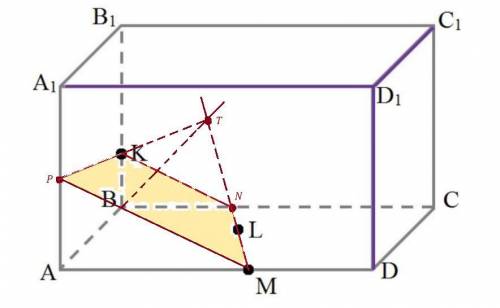
Соединим точки М и L , лежащие в одной плоскости ABCD . ML пересекается с ВС в точке N .
Продлим ML до пересечения с АВ , получим точку Т .
Теперь соединим точку Т и точку К , так как они лежат в одной плоскости АА1В1В . Продлим КТ до пересечения с АА1 в точке Р .
Соединим точки Р и М , так как они лежат в одной плоскости AA1D1D .
Получили сечение МNKP . Это трапеция, так как МР || KN в силу того, что если две параллельные плоскости ( АА1D1D и BB1C1C ) пересечены третьей ( MNKP ), то линии их пересечения параллельны.
АОС-СОВ=1/6(АОС-СОВ)
АОС-СОВ=1/6АОС-1/6СОВ
АОС-1/6АОС=СОВ-1\6СОВ
5/6АОС=7\6СОВ
АОС=7\5СОВ
7\5СОВ+СОВ=120
12\5СОВ=120
СОВ=120: 12/5
СОВ=50(град)
АОС=120-СОВ=120-50=70(град)