Объяснение:
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
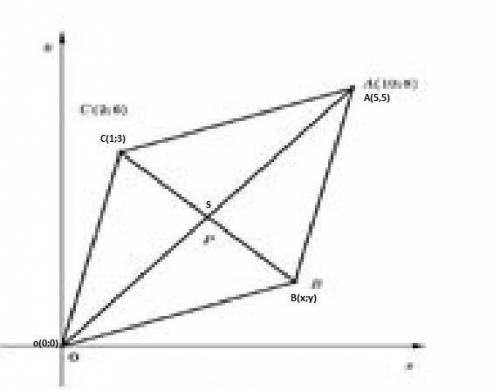
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)
Пусть О1, О2 и О3 - центры заданных окружностей с радиусами 12, 12 и 1 см.
Стороны треугольника с вершинами в этих точках равны 24 и 2 по 13 см.
Косинус угла α при вершинах О1 иО2 равен:
cos α = (24² + 13² - 13²)/(2*24*13) = 12/13.
Находим стороны АВ и АС треугольника АВС.
АВ = АС = √(12² + 12² -2*12*12*(12/13)) = 12√(2/13) см.
Сторона ВС из подобия равна: 24*(1/13) = 24/13 см.
Высота h треугольника АВС к стороне ВС равна:
h = √(АВ² - (ВС/2)²) = √((144*2/13) - (144/169)) = (12/13)√(26 - 1) = 60/13.
Площадь треугольника АВС равна:
S(АВС) = (1/2)*(24/13)*(60/13) = 720/169.
Радиус R окружности, описанной около треугольника ABC, равен:
R = (abc)/(4S) = ((12√(2/13))-(12√(2/13))*(24/13))/(4*(720/169)) = 1728/720 = 2,4 см.
DE=h*ctg60
DE=4√3*√3/3=4см
шукаємо АD
AD=12+4=16
2.DE=h*ctg60=2√3*√3/3=2см
AD=6+2*2=10