Объяснение:
Дано:
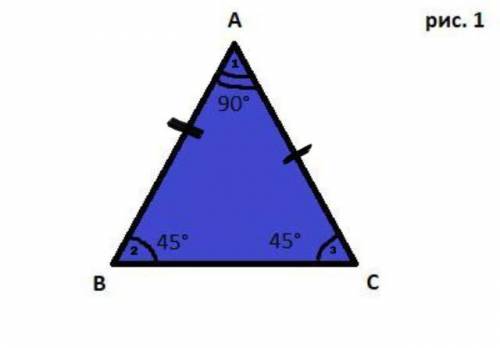
Δ ABC ----- равнобедренный.
∠ 1 ------ ?° в 2 раза больше ∠ 2.
Найти:
∠ 1; ∠ 2; ∠ 3.
Алгебраический решения № 1.
Пусть x° равен ∠ 2, тогда ∠ 1 будет равняться 2x°. Углы при основании равны (по свойству), поэтому ∠ 2 = ∠ 3 = x°. Сумма углов тр-ка 180°.
I этап. Составление математической модели:
x° + x° + 2x° = 180°
II этап. Работа с математической моделью:
2x + 2x = 180
4x = 180
x = 180 : 4
x = 45
III этап. ответ математической модели:
45° равен ∠ 2 и ∠ 3.
⇒ 2x = 2 * 45 = 90° равен ∠ 1.
Алгебраический решения № 2.
Пусть x° равен ∠ 2, тогда ∠ 1 будет равняться 2x°. Углы при основании равны (по свойству), поэтому ∠ 1 = ∠ 3 = 2x°. Сумма углов тр-ка 180°.
I этап. Составление математической модели:
x° + 2x° + 2x° = 180°
II этап. Работа с математической моделью:
3x + 2x = 180
5x = 180
x = 180 : 5
x = 36
III этап. ответ математической модели:
36° равен ∠ 2.
⇒ 2x = 2 * 36 = 72° равен ∠ 1 и ∠ 3.
1.
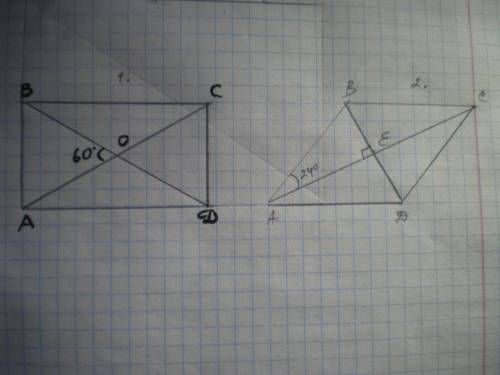
ABCD - прямоугольник, АС и BD - диагонали, ∠АВО=60°, BD=12 см,
АD=6√3 см. Найти Р.
ΔАОВ - равнобедренный, т.к. диагонали прямоугольника равны и в точке пересечения делятся пополам, АВ=АО=12:2=6 см
∠ВАО=∠АВО как углы при основании равнобедренного треугольника
∠ВАО+∠АВО=(180-∠АОВ):2=60°, значит, ΔАОВ - равносторонний, АВ=ОВ=АО=СD=6 см.
Р=2(6+6√3)=12+12√3=12(1+√3) см.
2.
Дано: АВСD - ромб, АС и ВD - диагонали, ∠ВАЕ=24°. Найти ∠АВD, ∠BAD, ∠DCB, ∠ADC.
Углы ромба делятся его диагоналями пополам, а противоположные углы ромба равны, поэтому
∠ВАD=∠BCD=24*2=48°
Сумма углов ромба, прилегающих к одной стороне, составляет 180°, поэтому ∠АВС=∠АDС=180-48=132°.
ответ: 48° 48° 132° 132°
ΔABF - прямоугольный, так как <CBF=60° (треугольник BCF правильный
- дано), <ABC = 30° - дано.
<ABF=<ABC+<CBF=30°+60°=90°.
АВ=BF=4, значит катеты равны и <BFA=<BAF=45°.
Тогда <OAC=<BAC-<BAF=75°-45°=30°.
Треугольник АОС равнобедренный (АО=ОС). Значит
ответ: в треугольнике АОС <OAC=<OCA=30°, <AOC=120°.
2. В ΔABC: Cos(HBC)=BH/BC => BH=BC*Cos15°=4*Cos15. BH=BF*Sin15°=4*Sin15.
В ΔBPF: Sin(BFP)=BP/BF =>BP=BF*Sin15°=4*Sin15.
Расстояние от АС до DF равно ВН-ВР или 4*Cos15-4*Sin15.
НР=4*(Cos15-Sin15)≈4*(0,966-0,259) ≈4*0,707 ≈ 2,8.
ответ: расстояние равно 4*(Cos15-Sin15)≈2,8.