Объяснение:
a) Ромб - параллелограмм, у которого все стороны равны, а углы непрямые.
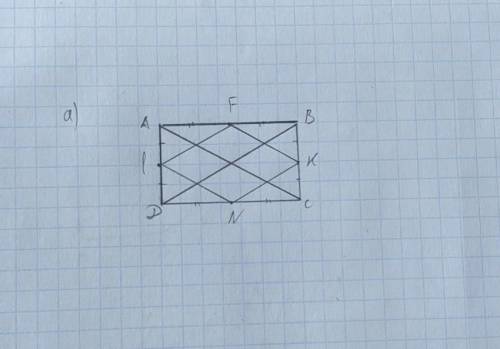
Рассмотрим ∆DAB:
LF - средняя линия треугольника, т.к AF=FB и AL=LD => LF // DB
Рассмотрим ∆BCD:
NK - средняя линия треугольника по таким же признакам, и NK // DB => и // LF.
В ∆ABC и ∆ADC FK // AC // LN по таким же признакам.
Мы знаем, что средняя линия треугольника равна половине основания этого треугольника, и по свойствам прямоугольника: AC=DB => и FK=KN=NL=LF
=> FKNL - ромб по определению. Ч.Т.Д.
б) мы можем свободно использовать равнобедренную трапецию, у которой диагонали равны, => доказательство соответствует пункту a)
ответ: на первое задание
Дано:
AO=OD
A=D
ДОКАЗАТЕЛЬСТВО:
так как уголAOB вертекален с углом COD угол О и там и там равен следовательно углы AOB И COD равны по теореме по 2м углам и прилижащей им стороне
Ч Т Д
ответ: на второе задание
ДОКАЗАТЕЛЬСТВО :
АБ=БЦ И АД=БЦ следовательно углы Д, Б равны друг другу 2. Следовательно треугольники АДЦ, АБЦ равны по теореме 2 стороны и угол между ними
Ч Т Д
ответ :на 3 задание
ДОКАЗАТЕЛЬСТВО :
ОБ это радиус окружности следовательно оба треугольника равнобедренные 2. Следовательно угол Б и там и там равен значит треугольники одинаковые по теореме 2 стороны и угол между ними
Ч Т Д
ОТВЕТ:на 4
ДОКАЗАТЕЛЬСТВО :
Рассмотрим треугольник МБО И ЦОН они вертикальные следовательно угол О и там и там равен 2. Следовательно треугольники МБО И ЦОН равны по теореме 2м углам и прилигающец к ним стороне 3. Следовательно треугольник БОЦ равнобедренный
Ч Т Д
ответ:на 5
ДОКАЗАТЕЛЬСТВО :
Так как треугольники ЦБА = ДАБ следовательно всех их стороны равны друг другу, следовательно ДБ = АС
Ч Т Д
Периметр: 46см*4=184 см^2