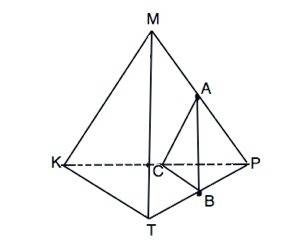
По условию секущая плоскость параллельна плоскости КМТ.
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
А Н Р Д
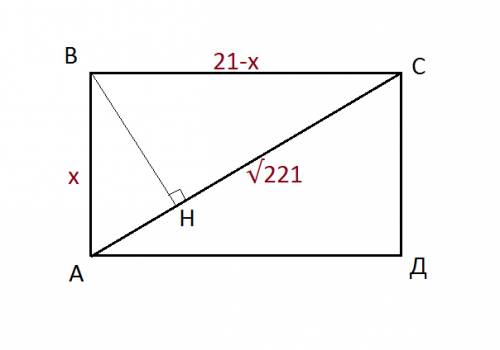
ВН, СР - высоты
уголА=углуД=45градусов
в треугольникеАВН уголАВН=180-90-45=45градусов => треугольник равнобедренный (АН=НВ=8см)
АН=РД=8см
ВС=НР=х
АД=8+х+8
Составляем уравнение по формуле средней линии:
(8+х+8+х):2=12
2х+16=24
2х=8
х=4см (ВС)
АД=8+4+8=20см