Решить 2 )основание трапеции относятся как 2: 3. ее средняя линия равна 24дм.найдите основания трапеции. 2)высота,опущенная из вершины тупого угла равнобедренной трапеции ,делит большее основание на 2 отрезка ,длины которых равны 3,5 и 8,5 дм. вычислите среднюю линию трапеции.

👇

Ответ:

GucciGang007

23.07.2020

1)Средняя линия трапеции равна полусумме её оснований. 24*2 =(2х+3х)
48=5х
х=9,6 дм. ответ:9,6 дм.
2) Проведём ещё одну высоту СH1, известная высота BH, трапеция ABCD.
Треугольники ABH и CDH1 равны ( AB=CD, CH=BH,угол ABH=H1CD)
Значит AH=H1d=3,5. Тогда верхнее основание будет равно : 8,5- 3,5*2=1,5
Cредняя линия будет равна= (8,5+1,5)/2= 5дм. ответ: 5дм. Удачи.

4,4(41 оценок)

Открыть все ответы

Ответ:

Islami1

23.07.2020

Предварительные вычисления.
Радиус вписанной окружности основания
r = √3/6·a
Радиус описанной окружности
R = √3/3·а
Площадь основания
S = √3/4·a²
а) Сечение параллельно основанию через середину высоты.
Треугольник этого сечения подобен треугольнику основания с коэффициентом подобия k = 0,5
Площадь сечения относится с площадью основания как k²
s₁ = S·k² = S/4 = √3/16·a²
б) Сечение проходит через боковое ребро и высоту
Основание треугольника сечения r+R, высота h
Площадь
s₂ = 1/2(r+R)h = 1/2(√3/6·a+√3/3·a)h = 1/2√3/2·ah = √3/4·ah
в) сечение через сторону основания перпендикулярно противоположному боковому ребру
В треугольнике из пункта и в текущем высота h₃ общая (на рисунке синяя). Найдём ей через площадь треугольника из пункта.
Нам нужна длина бокового ребра пирамиды
l² = h²+R² = h²+a²/3
l = √(h²+a²/3)
s₂ = 1/2 h₃l
√3/4·ah = 1/2 h₃√(h²+a²/3)
√3/2·ah = h₃√(h²+a²/3)
h₃ = √3·ah/(2√(h²+a²/3))
s₃ = 1/2·h₃a = √3·a²h/(4√(h²+a²/3)) = 3a²h/(4√(3h²+a²))
г) сечение через центр основания параллельно боковой грани
Треугольник этого сечения параллелен и подобен боковой грани пирамиды с коэффициентом подобия k = R/(R+r) = 2/3
Найдём плошадь боковой стороны
Её высота (синяя)
l² = h²+r² = h²+3/36·a² = h²+a²/12
l = √(h²+a²/12)
площадь боковой стороны
s = 1/2·al = 1/2·a√(h²+a²/12)
площадь сечения
s₄ = k²s = 4/9·1/2·a√(h²+a²/12) = 2/9·a√(h²+a²/12)
д) Сечение через середины четырех ребер
Такое сечение можно построить только проходящим через середины двух рёбер основания и двух боковых рёбер
Сечение имеет форму четырёхугольника (или равносторонняя трапеция или прямоугольник)
Нижнее ребро b₁ - средняя линия основания, его длина
b₁ = a/2
Боковое
b₂ и b₄ - средняя линия боковой грани и в два раза короче бокового ребра, длину его вычисляли раньше √(h²+a²/3)
b₂ = b₄ = (√(h²+a²/3))/2
верхнее ребро b₃ - средняя линия боковой грани, проведённая параллельно основанию, его длина
b₃ = a/2
Итого - у нас прямоугольник с площадью
s₅ = a/2·(√(h²+a²/3))/2 = (a√(h²+a²/3))/4

Вправильной треугольной пирамиде известны сторону основания a и высокая h. как вычислить площадь сеч

Вправильной треугольной пирамиде известны сторону основания a и высокая h. как вычислить площадь сеч

4,5(82 оценок)

Ответ:

костя663

23.07.2020

Дано АВСА₁В₁С₁- прямая призма? ∠С=90,СА=СВ,

АА₁=5см, S(бок. призмы)=10 см². Около призмы описан цилиндр

Найти R(цилиндра)

Объяснение:

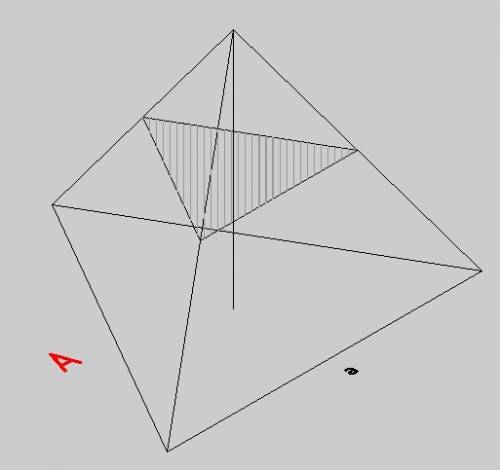
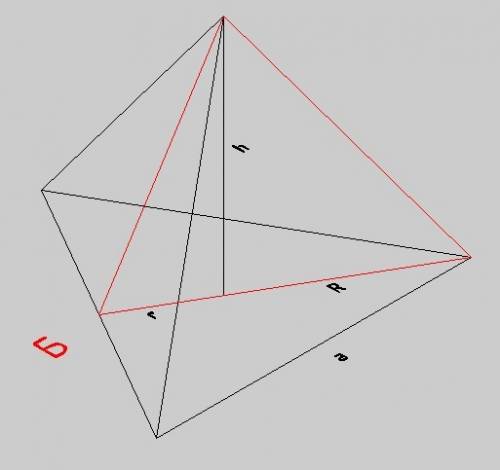
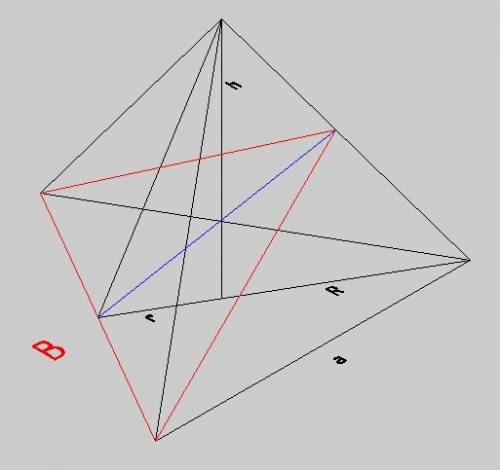
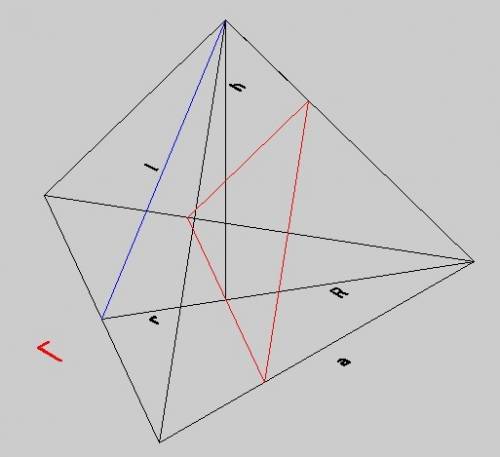
"Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра."

Т.к цилиндр описан около прямой призмы, то прямоугольный равнобедренный ΔАВС вписан в окружность , центр которой находится на середине гипотенузы. R=0,5*АВ.

Пусть катеты ΔАВС будут СА=СВ=х.

Тогда по т. Пифагора АВ²=х²+х² , АВ=2х², АВ= х√2 .

S(бок. призмы)=Р(осн)*h или

10 =(х+х+х√2)*5 или 10=х*(2+√2)*5 ,х=2/(2+√2)=2-√2 ( после избавления от иррациональности в знаменателе) ⇒

АВ=√2*(2-√2) =2√2-2 ,

R =(2√2-2):2=√2-1