1) в равностороннем треугольнике все высоты равны.
Верно.Это свойство высот равностороннего треугольника
2)точка пересечения медиан произвольного треугольника - это центр окружности, описанной около этого треугольника.
Неверно. Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника
4)медиана, это отрезок соеденяющий середины двух сторон треугольника.
Неверно. Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны
5) треугольник со сторонами 6,8,9- не существует.
Неверно. Существует.
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Проверим:
6+8>9, 14>9
8+9>6, 17>6
6+9>8, 15>8
6) треугольник со сторонами 3,4,5 -прямоугольный.
Верно. Он египетский.
Египетский треугольник - прямоугольный треугольник с соотношением сторон 3:4:5
ответ 1 и 6
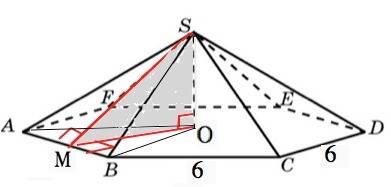
Основание правильной пирамиды - правильный многоугольник, а её вершина проецируется в центр многоугольника.
Для правильной шестиугольной пирамиды центр основания - точка пересечения её диагоналей.
Формула объёма пирамиды V=S•H:3
В основании данной пирамиды правильный шестиугольник, площадь которого равна площади 6-ти равносторонних треугольников.
Формула площади ∆ (АОВ)=a²√3/4.
SM=AB=6 см
S(основания)=6•S(AOB)=6•36√3/4=54√3 см²
Высоту ЅО найдем по т.Пифагора из прямоугольного ∆ SOM.
SO=√(SM²-OM²)
ОМ=ОВ•sin60°=6√3/2=3√3⇒
ЅО=√(36-27)=3 см
V=(54√3)•3:3=54√3 см³
Проведем через точку К прямые параллельные DC и DB, тогда плоскость NKP будет параллельной плоскости BDC.