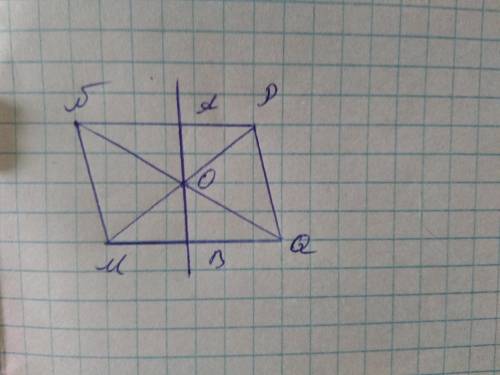
а) Рассмотрим ΔMBO и ΔAPO
1) ∠AOP=∠MOB - как вертикальные углы
2) ∠OMB=∠APO - как накрест лежащие углы при параллельных прямых NP и MQ и секущей MP. (NP//MQ - по определению параллелограмма)
3) MO=OP - по свойству параллелограмма (точкой пересечения делит диагонали пополам)
Значит ΔMBO и ΔAPO равны по двум углам и стороной между ними. Следовательно AO=OB - как соответственно равные элементы в равных треугольниках.
б) 1) Из пункта а) ΔMBO = ΔAPO, значит MB=AP=2 см - как соответственно равные элементы в равных треугольниках.
2) NP=NA+AP=3+2=5см
Объяснение:
Объяснение:
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).
АВ = 2 см
BC = 4 см
AB
2
+BC
2
=AC
2
2
2
+4
2
=AC
2
AC
2
=20
AC=2
5
cm
ответ: 2√5см.