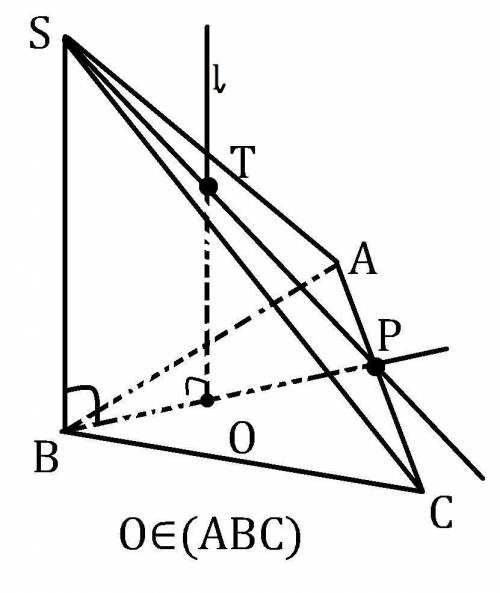
Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.
1. проводим прямму а (базовое построение)
2. обозначем точку А на пряммой а (базовое построение)
3. Через точку А проводим пряммую с, перпендикулярную пряммой а (базовая задача на построение)
4. Откладываем от точки А отрезки АС и АВ длиной равные данному отрезку 1. (базовое построени). Получим прямоугольный треугольник, гипотенуза которого равна ВС=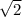
5. Продолжаем отрезок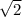 от точки С на отрезок равный данному, получим большой отрезок длинной ВР=1+\sqrt{2} (базовое построение)
от точки С на отрезок равный данному, получим большой отрезок длинной ВР=1+\sqrt{2} (базовое построение)
6. На єтой же пряммой далее от точки Р откладываем отрезок РК равный данному с длиной 1.
7. Делим отрезок ВК пополам (базовая задача на построение)
8. Из середины О отрезка ВК радиусом ВО проводим окружность (базовое построение)
9. Через точку Р проводим перпендикулярную пряммую РХ,(базовая задача на построение) она пересечет окружность в двух точках, берем одну из них обозначаем Н,
отрезок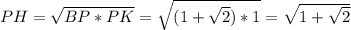 искомый
искомый