Дано:
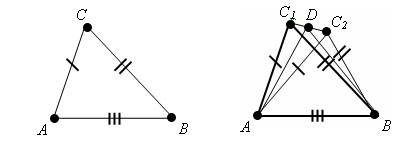
∠A=∠A1
AB=A1B1
AC=A1C1
Доказать:
ΔABC=ΔA1B1C1
Доказательство:
Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны. как то такв середине треугольник не нужен
![r= \frac{2}{ \sqrt[4]{2} \sqrt{\pi} } и R= \frac{10}{ \sqrt[4]{2}\ \sqrt{\pi} }](/tpl/images/4502/4506/2a430.png)
1
Обозначим центры оснований усечённого конуса через A и E, так что A – центр большего основания. Отметим на большем основании точку C, а точку меньшего основания, через которую проходит образующая, выходящая из C, обозначим через D.
2
Высота AE и образующая CD лежат в одной плоскости. Обозначим точку их пересечения через B. Так как AE – высота, то AE⊥CD и AE⊥AC. Рассмотрим прямоугольный треугольник BAC: в нём ∠BCA=45∘, тогда
3.(первоее фото)
4
Рассмотрим прямоугольный треугольник BED: так как ∠EBD=45∘, то
5.(первое фото)
6
тогда EA=AB−BE=R−r, DC=BC−BD=R2−r2=2(R−r). б о к Sбок=π(R+r)⋅I, где I – образующая, тогда
7(первое фото)