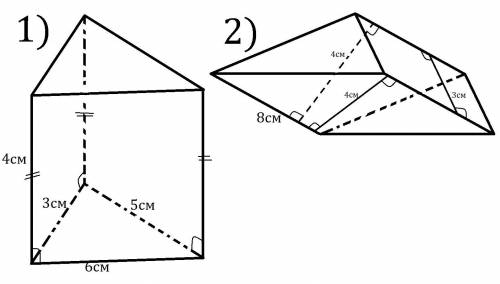
1)
Призма прямая, поэтому боковыми гранями будут прямоугольники. Одна их сторона это боковое ребро, а другая сторона это сторона основания. Найдём площадь боковой поверхности призмы как сумму площадей прямоугольников, которые составляют бок. пов.
S = 4см · 3см + 4см · 5см + 4см · 6см =
= 4см · (3см+5см+6см) = 4см · 14см = 56см².
ответ: 56см².
2)
Расстоянием между боковыми рёбрами призмы будет длина отрезка заключенного между боковыми рёбрами и лежащий на общем перпендикуляре. Боковые рёбра наклонной призмы это параллелограммы у которых мы знаем одну сторону (бок. реб.) и высоту проведённую к этой стороне (расстояние между бок. реб.), поэтому мы можем найти площадь параллелограмма. Площадь боковой поверхности найдём как сумму площадей параллелограммов, которые составляют бок. пов.
S = 8см · 3см + 8см · 4см + 8см · 5см =
= 8см · (3см + 4см + 5см) = 8см · 12см = 96см².
ответ: 96см².
Объяснение:
Дано: равносторонний треугольник АВС=треугольнику АСД. Доказать, что АВ || СD.
АВ=ВС=АС=АД=СД. Получили, что в четырехугольнике АВСД все стороны равны, значит этот четырехугольник является ромбом и к нему применимо свойство параллелограмма что его противоположные стороны попарно параллельны. Значит АВ || СD, что и требовалось доказать.
Дано: рівносторонній трикутник АВС=трикутнику АСД. Довести, що АВ || СD.
Рішення:
АВ=ВС=АС=АД=СД. Отримали, що в чотирикутнику АВСД всі сторони рівні, значить цей чотирикутник є ромбом і до нього застосовується властивість паралелограма що його протилежні сторони попарно паралельні. Значить АВ || СD, що і потрібно довести.