Объяснение:
1)
фото чертежа прилагаю.
Проведём высоту ВК.
sin 30°=BK/BC
1/2=BK/12
BK=12/2=6 см .
S(ABCD)=BK*(AB+DC)/2=6*(6+16)/2=
=6*11=66 см² площадь трапеции.
ответ: 66см²
2)
∆АВС- равносторонний по условию.
АВ=ВС=АВ.
Формула нахождения периметра равностороннего треугольника
Р=3*АВ
АВ=Р/3=18/3=6 см сторона треугольника.
S=AH*BC/2=3*6/2=9 см². площадь треугольника
ответ: площадь треугольника равна 9см²
3)
1) 80:2=40см полупериметр прямоугольника (АВ+ВС)
2) пусть сторона АВ=2х см, тогда сторона ВС=6х. Составляем уравнение.
2х+6х=40
8х=40
х=40/8
х=5
АВ=2х, подставляем значение х.
2*5=10см сторона АВ.
ВС=6х, подставляем значение х.
6*5=30 см сторона ВС
S=AB*BC=10*30=300см² площадь прямоугольника АВСD
ответ: 300см²

Задача 2.
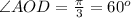
Задача 3.
Проекциями прямых параллельных сторонам исходного параллелограмма будут прямые, проходящие через т. пересечения диагоналей и середины сторон у параллелограмма проекции
Объяснение:
Дано
АВСД - прямоугольник
АВ = 6 см
АД = 2√3 см
Найти
уг. м/ду АС и ВД
Решение
Очевидно, что АС и ВД - диагонали прямоугольника.
Обозначим т. пересечения как т. О
Тогда уг.АОД - искомый угол между диагоналями.
Обозначим
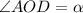
По св-вам прямоугольника, его диагонали равны и в т. пересечения делятся пополам. Т.е.
АО = ОС = ВО = ОД
По Т. Пифагора можно найти диагонали:
ВД² = АВ² + АД²
BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2}
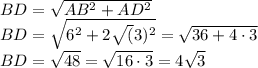
Соответственно
АС = ВД = 4√3Рассмотрим тогда треугольник АОД, он равнобедренный, т.к.
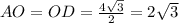
Так же 2√3 равна и сторона АД нашего прямоугольника.
То есть - мы получаем, что
АО = ОД = АД = 2√3
Следовательно - ∆АОД равносторонний,
а это означает, что искомый угол AOД
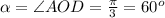
Для особо дотошных:
По Т. косинусов имеем:
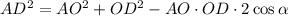
Отсюда
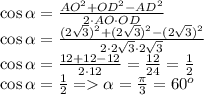
JL=ET
JM=EF
LM=TF
Объяснение:
там тип по порядку буквы идут и так и ответ