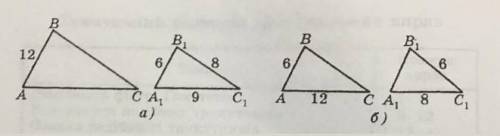
АBCD - трапеция, ∠B = 120°, BC = 4 cм, AB = 6 см, AB = CD. Найти площадь трапеции.
=============================================================
AB = CD ⇒ ABCD - равнобедренная трапецияОпустим высоты ВС и СН на основание AD, тогда∠ABE = ∠DCH = 120° - 90° = 30°В ΔАВЕ: sin30° = AE/AB ⇒ AE = AB•sin30° = 6/2 = 3 смAE = HD = 3 см, AD = AE + EH + HD = 3 + 4 + 3 = 10 смПо т. Пифагора: ВЕ² = АВ² - АЕ² = 6² - 3² = 36 - 9 = 27ВЕ = 3√3 смS abcd = (1/2)•(BC + AD)•BE = (1/2)•(4 + 10)•3√3 = 21√3 см²ОТВЕТ: 21√3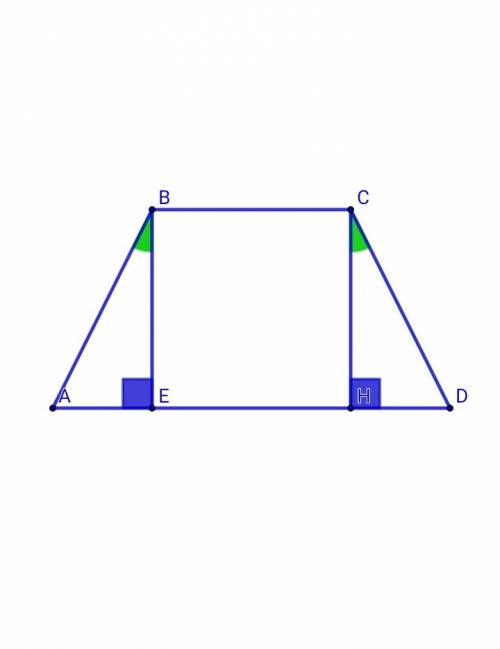
Объяснение:
а)
АВ/А1В1=ВС/В1С1=АС/А1С1
12/6=ВС/8
ВС=8*12/6=16
12/6=АС/9
АС=9*12/6=18
ответ: ВС=16; АС=18
б)
АС/А1С1=ВС/В1С1=АВ/А1В1
12/8=ВС/6
ВС=6*12/8=9
12/8=6/А1В1
А1В1=6*8/12=4
ответ: ВС=9; А1В1=4