Question

Цилиндр описан около шара.Найдите объём шара,если объём цилиндра 78​

Answer 1

Объём шара = 52

Объяснение:

Формула объёма шара:

$V=\frac{4}{3}\pi R^{2}$

Необходимо найти радиус шара.

У  шара и у цилиндра общий радиус. Основание цилиндра это круг с радиусом R, высота цилиндра равна двум радиусам. Значит объём цилиндра вычисляется по формуле:

$V=\pi R^{2} *2R$

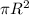где $\pi R^{2}$ - площадь основания цилиндра,

$2R$ - высота цилиндра

Подставим объём цилиндра = 78 из условия задачи в данную формулу, и выразим радиус:

$78 = \pi R^{2} *2R\\\\ 78 = 2\pi R^{3} \\\\ R^{3} = \frac{33}{2\pi }$

Оставим выражение в таком виде, выражать радиус (извлекать корень третьей степени) не обязательно, так как нам понадобится именно R³.

Таким образом, объём шара будет равен:

$V=\frac{4}{3} \pi R^{3}=\frac{4}{3}\pi *\frac{78}{2\pi} = \frac{2*78}{3} = 52$