128π√2/3 см³
Объяснение:
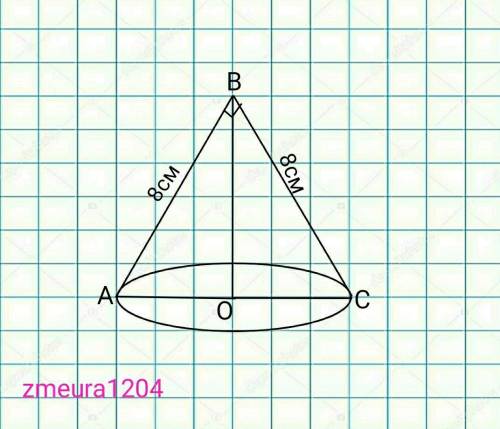
∆АВС- прямоугольный равнобедренный треугольник.
АС=АВ*√2=8√2 см диаметр.
АО=АС/2=8√2:2=4√2см радиус.
∆ABO- прямоугольный треугольник
Теорема Пифагора
BO=√(AB²-AO²)=√(8²-(4√2)²)=√(64-32)=
=√32=4√2 см высота конуса
V=⅓* Sосн*h=⅓*π*AO²*BO=
=⅓π*(4√2)²*4√2=128π√2/3 см³
ОбъясненВ правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Решение.
Введём обозначения, как показано на рисунке. Выразим длину стороны через длину боковой стороны Высота правильного треугольника выражается через его сторону: Точкой высота делится в отношении 2 : 1, поэтому Угол равен углу между боковой гранью и плоскостью основания. Из прямоугольного треугольника
Из прямоугольного треугольника по теореме Пифагора:
ответ: 8
ОбъясненВ правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Решение.
Введём обозначения, как показано на рисунке. Выразим длину стороны через длину боковой стороны Высота правильного треугольника выражается через его сторону: Точкой высота делится в отношении 2 : 1, поэтому Угол равен углу между боковой гранью и плоскостью основания. Из прямоугольного треугольника
Из прямоугольного треугольника по теореме Пифагора:
ответ: 8
Объяснение:
во вложении