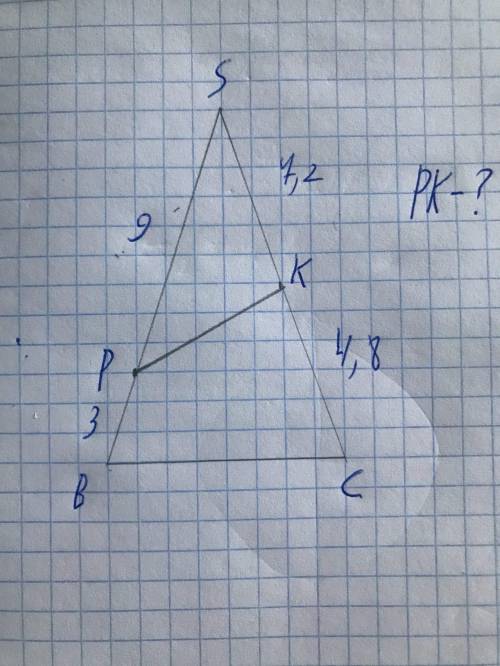
а) Если треугольник BKD прямоугольный, то мы можем применить к нему т. Пифагора: BK^2+KD^2=BD^2; BD^2=5^2+12^2=169; BD=кв.кор из 169=13 и по условию BD=13см, из этого следует что треугольник BKD-прямоугольный.
б) Мы доказали , то что треугольник BKD -прямоугольный с прямым углом K следственно треугольник ABK тоже прямоугольный. Площадь прямоугольного треугольника вычисляется по формуле S=1/2*Ak*BK=1/2*4*12=24см^2
AD=AK+KD=4+5=9 Площадь параллелограмма равна произведению основания на высоту; BK*AD=12*9=108см^2
4,5
Объяснение:
BS = 3+9=12
CS = 7,2+4,8=12
BC = 12
Треугольник равнобедренный, => каждый кут по 60°
Сторона противоположна куту 60° = половина гипотинузы
РК = 9:2=4,5 (см)