46
Объяснение: Пусть основания - меньшее ВС, большее АD.
Точка О -центр окружности , описанной около трапеции. По условию она находится внутри окружности. Она принадлежит отрезку соединяющему середины оснований. Длина этого отрезка равна заданной высоте трапеции.
Квадрат высоты треугольника ВОС равен по теореме Пифагора 17*17- 8*8=225 (8=половине меньшего основания).
Значит высота ВОС равна 15. Высота ОАD равна 23-15=8
Квадрат половины большего основания трапеции равен по теореме Пифагора
17*17-64=225. Значит большее основание равно 30.
Сумма оснований равна 46
ответ:
AD=DC=40 см
Объяснение:
Точка пересечения серединных перпендикуляров является одновременно центром описанной окружности, значит АС - её диаметр, откуда следует что R=AD=DC=80/2=40
Можно более длинным путём, но зато без окружности:
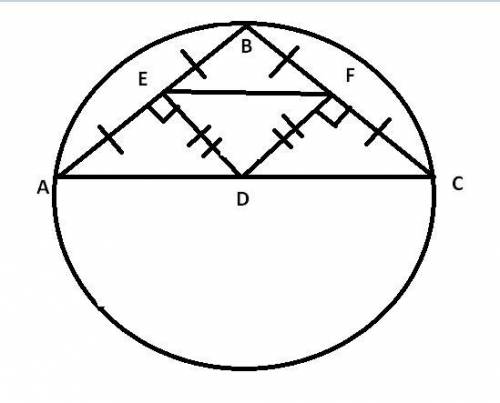
Проведём EF.
ΔEBF - равнобедренный, Значит ∠BEF=∠BFE;
∠DEF=∠EFD Т.к. 90-∠BEF=90-∠BFE ⇔ ΔDEF равнобедренный ⇔ ΔAED=ΔDFC по двум сторонам и углу между ними ⇔ AD=DC
а значит AC=2DC ⇔ DC=AC/2=80/2=40 см; AD=40 см
Буду признателен, если выберешь лучший ответ, чтобы я получил
Если периметр 52, то сторона 52/4=13/см/; диагонали в точке пересечения делятся пополам и пересекаются под прямым углом; половина данной диагонали 24/2=12/см/, тогда половина другой диагонали √(13²-12²)=√(25*1)=5/см/, диагонали равны 24 см и 5*2=10/см/, тогда площадь равна 0.5*10*24=120/см²/, и эта же площадь. с другой стороны, равна произведению стороны на высоту, проведенную к этой стороне, которая является диаметром окружности, вписанной в ромб.
откуда диаметр равен d=2r=120/13; значит, радиус искомый равен 120/(2*13)=60/13=4 8 /13/cм/