Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
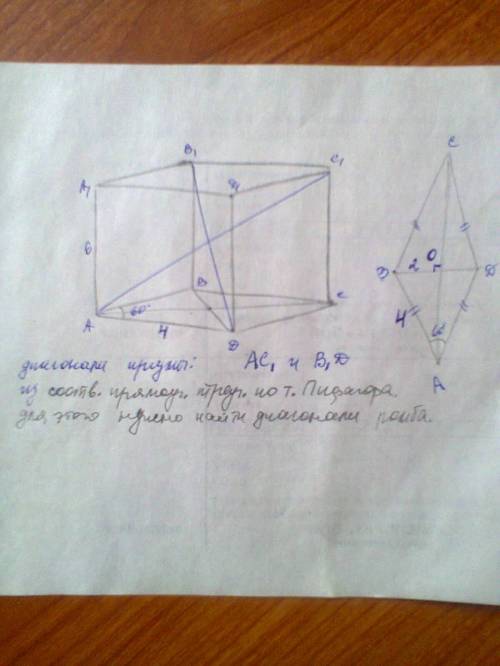
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
1) 0,1m + (m + m + 1) = 0,1m + m + m + 1 = 2,1m + 1
2) 2p² - (p² - 2pq + q) = 2p² - p² + 2pq - q = p² + 2pq - q.
Если перед скобкой стоит +, то скобки убираем, а знаки оставляем.
Если перед скобкой стоит -, то скобки убирает, а "+" меняем на "-", "-" меняем на "+".