20
Объяснение:
Объяснение:
Доказательство: Пусть даны две прямые a и b. Предположим, что они имеют более одной общей точки - точки M и N. Тогда через две точки M и N проходила бы не одна, а две прямые - прямые a и b. Но это противоречит аксиоме. Конец доказательства.
Что мне не нравится в доказательстве: Хорошо, мы доказали, что две разные прямые не могут иметь две общие точки. Но для меня ситуация выглядит так, что мы доказали только этот частный случай. А если мы возьмем три общие точки или больше? Не похоже, чтобы аксиома запрещяла, чтобы две разные прямые имели три общие точки.
Умом-то я понимаю, что если две прямые имеют более одной общей точки, то они являются одной и той же прямой. Но вот строго доказать, увы, не могу. И мне кажется, что для этого хватит все той же аксиомы. А вся моя проблема проистекает из-за неверного понимания самой аксиомы, которая скорее всего запрещяет и случаи с большим количеством общих точек.
МОЛОДЦЫ ДЕРЖИТЕСЬ УДАЧИ ВАМ -^-)
Объяснение:
3 .Нехай ІІ суміжний кут має х° , тоді І суміжний кут має 17х° .
Рівняння : 17х + х = 180° ;
18х = 180° ;
х = 10°.
В - дь : 10° .
4 . Нехай менший із утворених кутів має 2х° , тоді суміжний з ним кут 13х° .
Рівняння : 2х + 13х = 180° ;
15х = 180° ;
х = 180° : 15 ;
х = 12° ; 2х = 2*12 = 24° ; 13х = 13 * 12 = 156° .
В - дь : 24° , 156° , 24° , 156° .
5 . Нехай ∠EAF = x° , тоді ∠ВАС = 4х° .
Рівняння : 4х + 4х + х = 180° ;
9х = 180° ;
х = 20° ; ∠CAF = 4x + x = 5x = 5 * 20° = 100° .
В - дь : ∠CAF = 100° .
ответ: :20 см
Вариант решения.
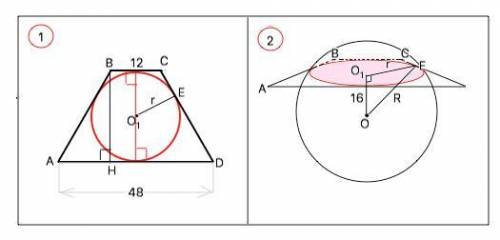
Объяснение. Любое сечение сферы плоскостью - окружность. Для трапеции, стороны которой касаются сферы, эта окружность - вписанная. Пусть данная трапеция АВСD, О - центр сферы, О₁ - центр окружности, по которой плоскость трапеции пересекает сферу. О₁Е - радиус окружности.
Если в четырехугольник можно вписать окружность, (соответственно, и если четырехугольник описан около окружности) то суммы его противоположных сторон равны.
Трапеция - четырёхугольник, описанный около окружности. ⇒ АВ+СD=BC+AD= 12+48=60. Трапеция равнобедренная ⇒ АВ=CD= 60:2=30.
Диаметр вписанной в трапеции окружности перпендикулярен основаниям в точках касания и равен её высоте.
Высота равнобедренной трапеции из тупого угла делит основание на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме. Высота трапеции ВН делит АD на АН и НD. АН=(АD-BC):2=(48-12):2=18(см). (см. рисунок).
Из прямоугольного ⊿ АВН по т.Пифагора ВН=√(АВ²-АН²)=√(900-324)=24 (см).
d=24, r=24:2=12 (см).
Расстояние от точки до плоскости равно длине отрезка, проведенного из точки перпендикулярно к плоскости. ⇒ Угол ОО1Е=90°.
Из ⊿ ОО1Е по т.Пифагора
R=ОЕ=√(ОО1²+О1Е² )=√(16²+12²)=20 (см)