1. Гипотенуза прямоугольного треугольника равна 9 см, катет равен 4,5 см. Определите градусные меры углов треугольника.
90 градусов , 30 гр, 60 гр
2.Гипотенуза прямоугольного треугольника равна 16 см, острый угол равен 30 градусов. Определите, чему равен катет, лежащий напротив этого угла.
16/2=8см
3.Определите градусную меру острых углов прямоугольного треугольника, если его катеты равны 4,45 см.
45 гр и 45 гр
4.Сколько высот можно провести из вершины прямого угла?
3
5.Один из углов прямоугольного треугольника на 54 градусов больше другого. Найти величины всех углов треугольника.
18,72,90
6.В треугольнике АВС угол С равен 90 градусов, угол В равен 60 градусов, АВ = 43 см. Чему равна сторона ВС?
21,5 см
7. В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 6, а BC =12.
30 градусов
пока только решение к заданию 327.
остальное решу и допишу
рис 231.
прямые m,n параллельны,т.к. соответвенные углы равны(по 100 град.); угол,смежный со вторым является соответственным углу 94 град.; значит угол 2+94=180град. угол2=180-94=86 град.
Объяснение:
Задание 330 рисунок к нему ниже
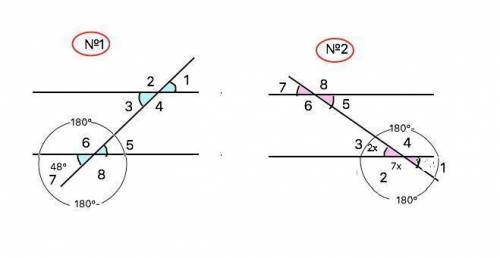
1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Задание 329
а ‖ b, с - секущая.
∟1 i ∟2 внутренние односторонние. ∟1> ∟2 в 4 раза.
Найти: ∟1; ∟2.
Пусть ∟2 = х; тогда ∟1 = 4х. Если а ‖ b, с - секущая,
тогда по признаку параллельности прямых имеем:
∟1 + ∟2 = 180 °.
Составим i решим уравнение:
4х + х = 180; 5х = 180; х = 180: 5;
х = 36 ∟2 = 36 °; ∟1 = 4 • 36 ° = 144 °
ответ. 36 ° и 144 °
Sз.ф.=375π+25√15π см²
V=1250π см³
Объяснение:
∆АВС- прямоугольный треугольник
<АСВ=90°
АВ=40см - гипотенуза
АС=10см - катет
По теореме Пифагора найдем
ВС=√(АВ²-АС²)=√(40²-10²)=√(1600-100)=
=√1500=10√15 см.
Проведём высоту СО в ∆АВС.
СО=ВС*СА/АВ=10*10√15/40=2,5√15 см
При вращении получили два конуса.
СО=R;
Sбок(КВС)=π*CO*BC=π*2,5√15*10√15=
=375π см²
Sбок(КАС)=π*СО*АС=2,5√15*10*π=
=25√15π см²
Sз.ф=Sбок(КВС)+Sбок(КАС)=375π+25√15π см² площадь заданной фигуры.
V=⅓*Sосн*h=⅓*π*OC²*AB=
=⅓*π*(2,5√15)²*40=⅓*93,75*40π=1250π см³