1.Объясните, какое утверждение называется аксиомой. Приведите примеры аксиом. Сформулируйте аксиому параллельных прямых. Сколько прямых можно провести через две точки? Какое утверждение называется следствием? Сформулируйте два следствия из аксиомы параллельных прямых. Докажите одно из них. 2.Дайте определение подобных треугольников. Сформулируйте и докажите теорему об отношении площадей подобных треугольников. Чему равно отношение периметров подобных треугольников? Что такое коэффициент подобия?
3.Какие стороны в подобных треугольниках называются сходственными? Сформулируйте три признака подобия треугольников. Докажите первый признак подобия треугольников.
4.Дайте определение синуса, косинуса и тангенса острого угла. Как обозначаются данные величины? Запишите формулу, как связаны между собой синус, косинус и тангенс острого угла? Сформулируйте и докажите как связаны синусы, косинусы и тангенсы острых углов в прямоугольных треугольниках, если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника.
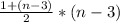и еще плюс (n-3)
Объяснение:
Дано: AB = A1B1, CH=C1H1, <CAH=<C1A1Н1. АН, А1Н1 - высоты.
Доказать: △АВС=△А1В1С1.
Док-во:
Рассмотрим △АСН и △А1С1Н1. Они прямоугольные и у них CH=C1H1 - катеты, <CAH=<C1A1Н1 - острые углы. Значит △АСН=△А1С1Н1 по 4 признаку (по катету и острому углу). => АС=А1С1, АН=А1Н1.
Рассмотрим △АВН и △А1В1Н1. Они прямоугольные и у них АН=А1Н1 - катеты, AB = A1B1 - гипотенузы. Значит △АВН=△А1В1Н1 по 2 признаку (по катету и гипотенузе). => ВН=В1Н1.
CH=C1H1, ВН=В1Н1, CB=CH+HB, C1B1=C1H1+H1B1 => CB=C1B1.
Таким образом для треугольников △АВС и △А1В1С1 имеем, что AB = A1B1, АС=А1С1, CB=C1B1, значит △АВС=△А1В1С1 по 3му признаку (по 3м сторонам), чтд.