Відповідь:
Пояснення:

Дано :
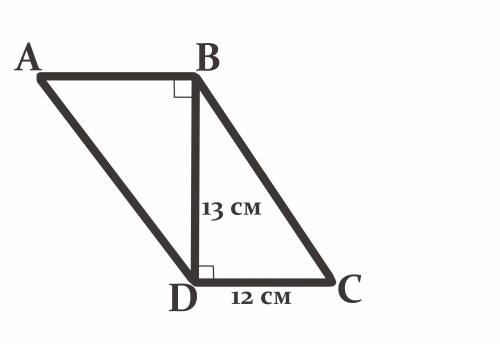
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
При пересечении двух параллельных прямых секущей могут образоваться несколько видов углов:соответсвенные,накрест лежащие и односторонние. Соответственные и накрест лежащие углы друг другу равны,поэтому к данной задаче не подходят,т.к по условию углы разные.Следовательно,данные углы являются односторонними.
Сумма односторонних углов равна 180°.
Дано: <1 и <2-односторонние,<2=5<1
Найти:<1,<2.
<1 +<2=180°
<1 + 5>1=180°
6<1=180°
<1=180°:6
<1= 30°
<2=5•<1=5•30°=150°
При пересечении двух параллельных прямых секущей образуется 8 углов.
На рисунке углы ∠3 и ∠6 являются внутренними накрест лежащими, как и углы ∠4 и ∠5.
Углы ∠3 и ∠5 являются внутренними односторонними, как и углы ∠4 и ∠6.
Пары соответственных углов следующие: ∠1 и ∠5, ∠3 и ∠7, ∠2 и ∠6, ∠4 и ∠8.