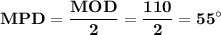По теореме косинусов:
с² = a² + b² - 2ab·cos∠C = 4 + 16 - 2 · 2 · 4 · cos∠C
25 = 20 - 16cos∠C
16cos∠C = - 5
cos∠C = - 5/16 = - 0,3125
Так как косинус угла С отрицательный, то угол тупой. По таблице Брадиса находим, что если cosα = 0,3125, то α ≈ 72°, тогда
∠C ≈ 180° - 72° ≈ 108°
По теореме косинусов:
a² = b² + c² - 2bc·cos∠A
4 = 14 + 25 - 2 · 4 · 5 · cos∠A
40cos∠A = 35
cos∠A = 35/40 = 7/8 = 0,875
∠А ≈ 29°
Сумма углов треугольника равна 180°, поэтому
∠В = 180° - (∠А + ∠С) ≈ 180° - (29° + 108°) ≈ 43°
Площадь треугольника найдем по формуле:
S = 1/2 ac·sin∠B
sin∠B ≈ 0,682
S ≈ 1/2 · 2 · 5 · 0,682 ≈ 3,41 см²
Р=3R*sqrt(3)
Откуда
R=P/3*sqrt(3)=45/3*sqrt(3)=15*sqrt(3)
Радиус окружности описанной около восьмиугольника определяется по формуле
R=a/2sin(360/16)=a/2sin(22,5°)
Откуда
a=R*2sin(22,5°)=2*15*sqrt(3)*sin(22,5°)=30*1,7*0,38=19,38
2. Площадь квадрата равна
S=a^2
Определим радиус окружности
R^2=a^2+a^2=2a^2
Площадь круга равна
Sк=pi*R^2=2*pi*a^2=144*pi
3. L=pi*r*a/180, где a – градусная мера дуги, r- радиус окружности
L=pi*3*150/180=2,5*pi
4. Сторона квадрата равна p/4=48/4=12
Диагональ квадрата равна
d^2=a^2+a^2=144+144=288
d=12*sqrt(2)
Радиус квадрата вписанного в окружность равна
R=d/2=6*sqrt(2)
Сторона правильного пятиугольника L, вписанная в эту окружность равна
L=2R*sin(36°)=12*sqrt(2)*sin(36°)=12*1,4*0,588=9,88
5. Площадь кольца находим по формуле:
S=pi* (R^2−r^)
S=pi*(7^2-3^2)=pi*(49-9)=40*pi
6. Треугольник равносторонний, так как угол равен 60°, радиус окружности равен 4
Найдем площадь треугольника по формуле
Sт=R^2*sqrt(3)/4
Sт=16*sqrt(3)/4=4*sqrt(3)
Найдем площадь сектора по формуле
Sc=pi*R^2*(60/360)=pi*16/6==8*pi/3
Найдем площадь сегмента
Sсм=Sс-Sт=8*pi/3-4*sqrt(3)=1,449
ответ: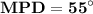
Объяснение: Проведем радиусы к точкам M и D теперь стоит заметить что стороны AC и AB являются касательными из чего исходя углы AMO и ADO прямые тогда MOD=360-70-90-90=110 ° теперь важно заметить что угол MOD центральный а угол MPD вписанный у вписанного угла есть свойство он равен половине центрального из чего выходит что