Дано: 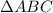
AB = BC = AC
AK - медиана
ВК = СК = 8дм
__________________
Найти AB, AC, BC.
1) Раз ВК и СК 8дм, значит по теореме о сумме отрезков ВС = ВК + СК = 8дм + 8дм = 16 дм
2) Раз АС = ВС = АВ (по условию), а ВС = 16дм (по 1 пункту моего решения), то АС = АВ = ВС = 16 дм.
ответ: АС = ВС = АВ = 16дм.
Дано: 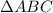
AB = BC = AC
AK - медиана
ВК = СК = 8дм
__________________
Найти AB, AC, BC.
1) Раз ВК и СК 8дм, значит по теореме о сумме отрезков ВС = ВК + СК = 8дм + 8дм = 16 дм
2) Раз АС = ВС = АВ (по условию), а ВС = 16дм (по 1 пункту моего решения), то АС = АВ = ВС = 16 дм.
ответ: АС = ВС = АВ = 16дм.
Если 5,76 см², то и ответ будет в см: 2,4см
Объяснение:
Дано:
АВDC - трапеция
AD = BC
АС ⊥ DB
EF - средняя линия
Sтр. = 5,76см²
h - ? EF - ?
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Построим высоту ЕF⊥ АВ .
Sтр = (a + b)/2 * h, где a и b - основания трапеции.
Sтр = h* (АВ * DC)/2 = 5,76см²
1) Теорема: если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований, т.е.
h = (АВ * DC)/2, тогда
Sтр = h* (АВ * DC)/2 =h*h = h² = 5,76см², откуда
h = √5,76 = 2,4см
2) Средняя линия трапеции - отрезок, соединяющий середины боковых сторон и расположенный параллельно основаниям. Длина средней линии, равна полусумме оснований.
ЕF = (АВ * DC)/2 = h = 2,4 см (рис.2)
(На рис. 2 лучше измените буквы F и Е на другие, например, К и М.
Тогда средняя линия будет КМ = (АВ * DC)/2 = h = 2,4 см
А то получилось и выосота и ср. линия с одинаковыми буквами)