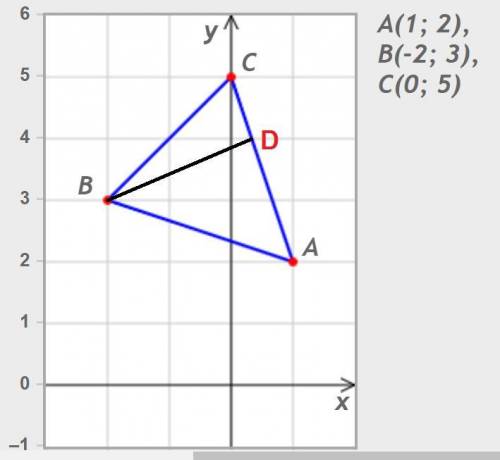
Даны вершины треугольника ABC: A (1; 2) B (-2; 3) и C (0; 5).
а) Найдите длину AB.
б) Найдите длину BC.
в) Найдите длину AC.
а,б,в) Вычислим длины сторон:
|AB|=√((xB−xA)²+(yB−yA)²) =√((−2−1)²+(3−2)²) = √((−3)²+1²) = √(9+1) =√10 ≈3,162;
|AC|=√((xC−xA)²+(yC−yA)²) =√((0−1)²+(5−2)²) = √((−1)²+3²) =√(1+9) =√10≈3,162;
|BC|=√(xC−xB)²+(yC−yB)²) = √((0−(−2))²+(5−3)²) = √(2²+2²) = √(4+4)= =√8 =2√2 ≈ 2,828.
г) Какова длина высоты BD?
д) Найдите площадь треугольника.
Зная длины сторон, по формуле Герона S = √(p(p-a)(p-b)(p-c)) находим площадь треугольника АВС. Полупериметр p = 4,576491223.
Подставив найденные значения в формулу, находим площадь.
S = 4 кв.ед.
По формуле S = (1/2)ah находим h = 2S/a.
Подставим данные: BD = h = 2*S/AC = 2*4/(√10) =8/√10 = 4√10/5 ≈ 2,529822128.
1)Найдите координаты точки пересечения прямых, заданными уравнениями
x+2y-5=0
3x-y-8=0
x+2y-5=0
3x-y-8=0
х=5-2у
3(5-2у)-у-8=0
15-6у-у-8=0
-7у=-7
у=1
х=5-2*1=3
ответ:(3;1)
2) В каких точках пересекается с осями координат прямая заданная уравнением:
2x-5y+20=0
при х=0 2*0-5у+20=0 Итак, первая точка (0;4)
5у=20
у=4
при у=0 2х-5*0+20=0 Итак, вторая точка (10;0)
2х=20
х=10
ответ: (0;4), (10;0)
3)Прямые y=x+4, y=-2x+1 пересекаются в некоторой точке О, найдите ее координаты.
х+4=-2х+1
х+2х=1-4
3х=-3
х=-1
у(-1)=-1+4=3
ответ: (-1;3)
36/π см или приблизительно 11,5 см.
Объяснение:
Если l - длина дуги окружности,. то
l = πRn / 180.
В нашем случае
3 = πR•15/180
3 = πR/12
πR = 36
R = 36/π (см).