Задание 1.
Пусть наибольший угол равен 3x, тогда по условию второй угол равен x.
Сумма смежных углов равна 180°.
3x+x = 180° = 4x
3x = 180° : 4 · 3 = 45°·3 = 135°
ответ: 135°.
Задание 2.
Пусть один угол равен x, тогда другой 0,8·x.
x+0,8x = 180° = 1,8x
x = 180° : 1,8 = 100°
0,8x = 0,8·100° = 80°
ответ: 80° и 100°.
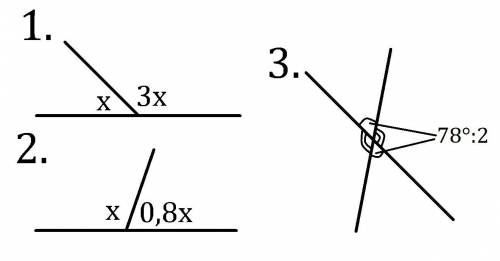
Задание 3.
В условии идёт речь про сумму противоположных углов т.к. смежные углы дают в сумме 180°, а не 78°.
Противоположные углы, при пересечении двух прямых, равны. Поэтому два угла, сумма которых 78°, равны 78°:2=39°. Смежные с ними углы так же равны между собой, а как смежные они равны 180°-39° = 141°.
ответ: 141°.
АВСД - параллелограмм, АД=ВС , АВ=СД , АД║ВС , АВ║СД .
∠АВС=110° ⇒ ∠ВАД=180°-110°=70° , ∠BCD=∠BAD=70° .
∠LAD=10° , тогда ∠BAL=70°-∠ДАL=70°-10°=60° .
∠KCD=10° , тогда ∠ВСК=∠ВСD-∠KCD=70°-10°=60° .
Рассмотрим два треугольника: ΔABL и ΔBCK .
Так как в ΔABL две стороны равны АВ=АL по условию , то ΔABL -равнобедренный. А так как ещё и угол в равнобедренном треугольнике ∠ВАL=60°, то этот треугольник - равносторонний, следовательно ВL=AB=AL=CD, ∠АВL=60° ⇒
∠CBL=110°-∠ABL=110°-60°=50° .
Аналогично, ΔВСК - равносторонний (КС=ВС по условию и ∠ВСК=60°) , следовательно ВК=ВС=СК=AD, ∠KBC=60° ⇒
∠KBL=∠KBC-∠CBL=60°-50°=10° .
Теперь рассмотрим три равных треугольника: ΔADL=ΔKCD=ΔKBL . Они равны по 1 признаку равенства треугольников:
AD=KC=BK , AL=CD=BL , ∠LAD=∠KCD=∠KBL=10° .
Отсюда следует, что стороны LD=KD=KL ⇒ ΔKLD - равносторонний, а в равностороннем треугольнике все углы равны 60°.
Значит, искомый угол ∠KDL=60° .