
1.Проводим высоту к стороне МК назовем ее NА и проведем высоту к стороне КР и обозначим ВQ.NA=2,a BQ=6.Площадь равна 48(по условию)
По формуле S=a•h мы можем узнать сторону МК=48:2=24,КР=48:6=8,следовательно Р=24+24+8+8=64
ответ:64
2.По теореме Пифагора
DF^2(в квадрате)=100-64=36
DF=6
По формуле найдем площадь треугольника:
S=1/2(дробь)•а•б=1/2•6°8=3•8=24(1/2 сократили с 6 и от 6 осталось 3)
ответ:24
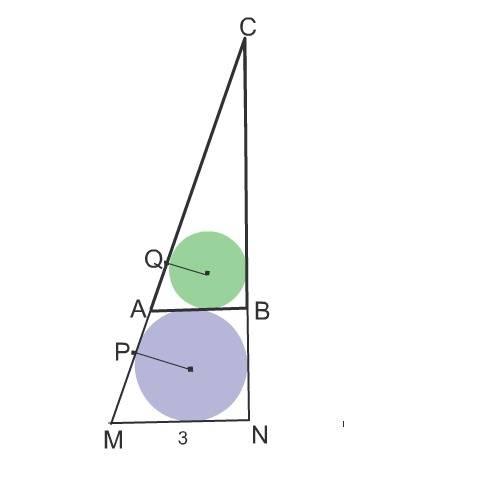
Так как MN║АВ, четырехугольник АВNM - трапеция.
В трапецию можно вписать окружность только тогда, когда суммы противоположных сторон равны.
АВ+MN=AM+BN
Периметр СМN= периметр АВС- АВ+3+AM+BN =Р АВС- АВ+3+(АВ+3)=12+6=18
ᐃ АВС ~ ᐃ MСN по свойству углов при пересечении параллельных прямых секущей и общему углу С.
Отношение периметров подобных треугольников равно отношению его сторон.
Р ᐃ MСN: Р ᐃ АВС=18:12=1,5
MN:АВ=1,5
3:АВ=1,5
АВ=3:1,5=2 см ( вообще-то не пригодится)
----
Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно его полупериметру :
СР=12:2=6см
Поскольку ᐃ АВС ~ ᐃ MСN, все их соответственные части имеют равный коэффициент подобия.
СР:СQ=1,5
6:СQ=1,5
СQ=6:1,5=4 см
РQ=СР- СQ=6 -4=2 см
Так как CL - биссектриса прямого угла С, то
∠ACL = ∠LCB = 90° : 2 = 45°;
2) ∠MCB = ∠LCB - ∠LCM = 45° - 15° = 30°
3) Используем свойство : медиана CM, опущенная на гипотенузу прямоугольного треугольника AB, равна половине гипотенузы.
АМ = МВ = СМ.
4) ΔСМВ - равнобедренный, так как СМ=МВ, значит углы при основании равнобедренного треугольника тоже равны:
∠СМВ = ∠МВС = 30°.
5) ∠САВ = 90° - 30° = 60°;
6) ΔАНС - прямоугольный (с прямым углом Н), так как СН - высота.
∠АСН = 90- 60=30°.
7) ∠LCH = ∠ACL - ∠ACH = 45° - 30° = 15°/
ответ: величина угла LCH = 15°.
Объяснение:
1)
S=h1*MK
MK=S/h1=48/2=24
S=h2*KP
KP=S/h2=48/6=8
P(MNPK)=2(MK+KP)=2(24+8)=2*32=64
ответ: 64
2)
Теорема Пифагора
DF=√(DE²-FЕ²)=√(10²-8²)=√(100-64)=
=√36=6
Площадь прямоугольного треугольника равна половине произведения двух катетов.
S=½*DF*FЕ=½*8*6=24
ответ: 24