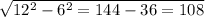
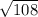
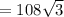
В кубе ABCDA1B1C1D1 найдите угол между векторами:
a)AB и AD , б)BB1 и CC1 , в)AC1 и A1D1
Объяснение:
Углы между векторами а)∠АВ,АD=90°, т.к все грани куба являются квадратами.
б) ∠ВВ₁,СС₁=0°, т.к эти вектора лежат на параллельных прямых.
в) ∠АС₁,А₁D₁=arcctg√2.
Т.к. вектор А₁D₁=AD , то найдем угол ∠АС₁,АD
Из ΔВСС₁ -прямоугольный. Пусть ребро куба а, тогда по т. Пифагора
ВС₁=а√2.
По т. о трех перпендикулярах если проекция ВС перпендикулярна , прямой лежащей в плоскости АВ, то и наклонная С₁В перпендикулярна прямой лежащей в плоскости АВ⇒ ΔАВС₁-прямоугольный .
tg∠С₁FD=BС₁/AB или tg∠С₁FD=а√2/а , tg∠С₁FD=√2 , ∠С₁FD=arctg√2,
а значит у угол между векторами ∠АС₁,А₁D₁=arcctg√2.
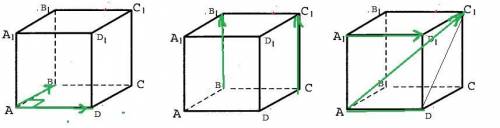
Вместо того, чтобы проводить отрезок CM (см. чертеж), я построил окружность на AC, как на диаметре. Середина AC - точка N - это центр этой окружности. Эта окружность проходит через все точки, из которых AC видна под прямым уголом, в частности - через точки D и F (основание высоты, в решении не нужна :) ).
Отрезок DE из условия является касательной к это окружности в точке D, так как ND II CB, как средняя линия треугольника ABC, то есть DE перпендикулярно радиусу ND.
В том числе эта окружность пересекает AE в точке K (из неё AC тоже видна под прямым углом, то есть ∠CKA = 90°). Я провожу отрезки CK и KM (M - середина DE), не предполагая, что они лежат на одной прямой. Для того, чтобы это "случилось", необходимо, чтобы ∠EKM = 90°. Вот это я и буду доказывать.
Треугольники AED и DKE подобны по 2 углам (один угол общий, а ∠KAD = ∠KDE, поскольку один угол вписаный, а другой лежит между касательной и секущей, и оба измеряются половиной дуги DK.
ND делит отрезок AE пополам (как средняя линия тр-ка ABC, ND делит пополам любую чевиану из вершины A), то есть Q - середина AE. Точки Q и M являются соответственными точками двух подобных треугольников, поэтому ∠QDE = ∠MKE = 90° чтд.
Если слова "являются соответственными точками" не понятны, то можно и так сказать - треугольники QDE и MKE подобны по двум пропорциональным сторонам и общему углу: QE и ME являются половинами сторон подобных треугольников AED и DKE, поэтому QE/ME = AE/ED = ED/EK;