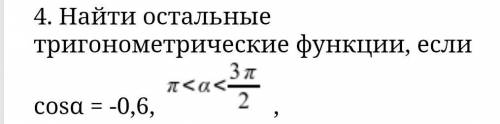
Дано четырехугольник ABCD с вершинами в точках A (1 , - 5) , B (2 , 3) , C (- 3 , 1) , D (- 4 , - 7) и нам нужно доказать , что это четырехугольник является параллелограммом .
Мы доказываем с свойству четырехугольника . Знаем , если координаты середин отрезков AC и BD совпадают , то это четырехугольник ABCD является параллелограммом .
Найдём середин отрезков AC и BD :
а) A (1 , - 5) ; C (- 3 , 1) :
x = (1 - 3)/2 = - 1 ; y = (- 5 + 1)/2 = - 2 .
б) B (2 , 3) и D (- 4 , - 7) :
x = (2 - 4)/2 = - 1 ; y = (3 - 7)/2 = - 2 .
Видно координаты середин одинаковы , значит , четырехугольник ABCD является параллелограммом .
ответ : Четырехугольник ABCD является параллелограммом .
5
Объяснение:
Чертёж в прикрепленном файле
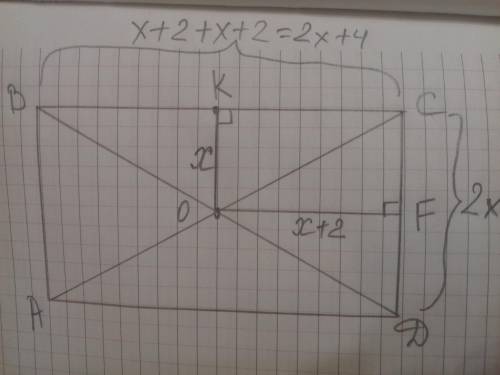
Диагонали прямоугольника равны и точкой пересечения делятся пополам, образуя равнобедренные треугольники. Расстояние от точки О до сторон прямоугольника является высотами в равнобедренных треугольниках, а значит и медианами. Образовавшийся четырехугольник OKCF - прямоугольник, КО=СF= х; КС=OF= х+2,
тогда DA=ВС= ВК+КС = х+2+х+2=2х+4; AB=CD=СF+FD= х + х=2х
Периметр прямоугольника Р=АВ+ВС+СD+DA= 2х+2х+4+2х+2х+4=8х+8
По условию Р=28
8х+8=28
8х=20 разделим обе части на 4
2х=5
т.к. меньшие стороны AB=CD=2х, значит меньшая сторона равна 5.
Угол в третьей четверти, поэтому синус там будет отрицательным, а тангенс и котангенс положительными. Значения этих тригонометрических функций по абсолютной величине проще всего искать с прямоугольного треугольника. Берем прямоугольный треугольник с катетом 3 (он будет выступать как прилежащий катет) и гипотенузой 5 (тогда косинус будет равен 3/5=0,6. Второй катет (противолежащий) будет равен 4 (здесь или Пифагор применяется, или мы вспоминаем египетский треугольник 3-4-5). Поэтому синус как отношение противолежащего катета к гипотенузе равен 4/5=0,8 (не забываем в окончательном ответе дописать минус), тангенс как отношение противолежащего катета к прилежащему равен 4/3, котангенс равен 3/4=0,75.